4
Modeling/Experimentation
The Synthetic Strategy in the Study of Genetic Circuits
Tarja Knuuttila and Andrea Loettgers
In philosophical discussions, models have been located between theories and experiments, often as some sort of go-betweens facilitating the points of contact between the two. Although the relationship between models and theories may seem closer than the one between models and experimentation, there is a growing body of literature that focuses on the similarities (and differences) between modeling and experimentation. The central questions of this discussion have concerned the common characteristics shared by modeling and experimenting as well as the various ways in which the inferences licensed by them are justified (e.g., Morgan 2003; Morrison 2009; Parker 2009; Winsberg 2009). Even though at the level of scientific practice scientists usually have no problem of distinguishing models and simulations from experiments, it has turned out difficult to characterize philosophically their distinctive features. In what follows we will attempt to clarify these issues by taking a cue from Peschard (2012) and considering the relationship of modeling and experimentation through a case in which they are used “in a tandem configuration” as Peschard (2013) puts it. We will study a particular modeling practice in the field of synthetic biology, whereby scientists study genetic circuits through a combination of experiments, mathematical models and their simulations, and synthetic models.[1]
With synthetic models we refer, in this context, to engineered genetic circuits that are built from genetic material and implemented in a natural cell environment.[2] In the study of genetic circuits they mediate between mathematical modeling and experimentation. Thus, an inquiry into how and why researchers in the field of synthetic biology construct and use synthetic models seems illuminating as regards the distinct features of modeling and experimentation.
Moreover, what makes the modeling practice of synthetic biology especially interesting for studying modeling and experimentation is that there is often no division of labor in synthetic biology laboratories: the same scientists typically engage in mathematical and synthetic modeling, and oftentimes even in experimentation. Consequently, one might expect that there are good reasons why synthetic biologists proceed in such a combinational manner. We argue that the gap between mathematical modeling and experimentation gave rise to the construction of synthetic models that are built from genetic material using mathematical models as blueprints. These hybrid entities share characteristics of both experiments and models, serving to make clearer the characteristic features of the two. Our empirical case is based, apart from the published journal articles in the field of synthetic biology, on interviews conducted with some leading synthetic biologists and a laboratory study of research performed at the Elowitz Lab at the California Institute of Technology. Elowitz Lab is known for its cutting-edge study of genetic circuits.[3]
We will begin by reviewing the philosophical discussion of the relationship of modeling and experimentation (in the second section). After that we will consider the contributions of mathematical modeling, experimentation, and synthetic modeling to the study of gene regulation. We will focus, in particular, on two synthetic models and how their combination with mathematical modeling gave researchers new insights that would have been unexpected on the basis of mathematical modeling alone (the third section). In the final section we discuss the characteristic features of modeling and experimentation, largely based on the previous discussion of the hybrid nature of synthetic models.
Modeling versus Experimentation
The experimental side of models as a distinct topic has largely emerged within the practice-oriented studies on modeling. Several philosophers have noted the experimental side of models, yet there has emerged no consensus on whether modeling and experimentation could or could not be clearly distinguished from each other. While some philosophers think that there are crucial differences between modeling and experimentation in terms of their respective targets, epistemic results, or materiality, others have presented counterarguments that have largely run modeling/simulation and experimentation together. In the following we will review this discussion, raising especially those topics that are relevant for synthetic modeling.
The recent philosophical discussion has pointed out three ways in which modeling and simulation resemble each other. First of all, one can consider them as largely analogous operations aiming to isolate some core causal factors and their effects. This argument has been presented in the context of mathematical modeling. Second, in dealing with simulation, numerous philosophers and scientists alike have pointed out their experimental nature as kinds of “numerical experiments.” The stress here is on intervention rather than on isolation. Also the fact that simulations are performed on a material device, the digital computer, has led some philosophers to liken them to experiments. A third motivation for claiming that the practices of modeling and experimentation are similar to each other invokes the fact that both simulationists and experimentalists produce data and are dealing with data analysis and error management (see Winsberg 2003, and Barberousse, Franceschelli, and Imbert 2009, for somewhat divergent views on this matter). We will not discuss this point further; rather, we will concentrate on isolation and intervention.
According to the argument from isolation, both in modeling and in experimentation one aims to seal off the influence of other causal factors in order to study how a causal factor operates on its own. In experimentation this sealing off happens through experimental controls, but modelers use various techniques such as abstraction, idealization, and omission as vehicles of isolation (see, e.g., Cartwright 1999; Mäki 2005). Consequently, a theoretical model can be considered as an outcome of the method of isolation: in modeling, a set of elements is theoretically removed from the influence of other elements through the use of a variety of unrealistic assumptions (Mäki 1992).
One central problem of the isolationist view is due to the fact that the idealizing and simplifying assumptions made in modeling are often driven by the requirements of tractability rather than those of isolation. The model assumptions do not merely neutralize the effect of the other causal factors but rather construct the modeled situation in such a way that it can be conveniently mathematically modeled (see, e.g., Cartwright 1999; Morrison 2008). This feature of mathematical models is further enhanced by their use of general, cross-disciplinary computational templates that are, in the modeling process, adjusted to fit the field of application (Humphreys 2004; Knuuttila and Loettgers 2012, 2014, 2016a, 2016b). Such templates are often transferred from other disciplines, as in the case of the research on genetic circuits where many models, formal methods, and related concepts originate from physics and engineering (e.g., the concepts of oscillator, feedback mechanism, and noise, as we discuss later).
The second sense in which models and experiments may resemble each other is due to the fact that in both modeling and experimentation one seeks to intervene on a system in the light of the results of this intervention. Herein lies the idea that simulations are experiments performed on mathematical models. But the question is how deep this resemblance cuts. Two issues in particular have sparked discussion: the supposed target systems of simulations versus experiments, and the role of materiality they incorporate.
A common intuition seems to be that, whereas in experimentation one intervenes on the real target system of interest, in modeling one merely interacts with a model system (e.g., Gilbert and Troitzsch 1999; Barberousse, Franceschelli, and Imbert 2009). Yet a closer examination has assured several philosophers that these intuitions may be deceptive. Winsberg (2009) argues that both “experiments and simulations have objects on the one hand and targets on the other, and that, in each case, one has to argue that the object is suitable for studying the target” (579; see also Guala 2002). Thus, both experimentation and modeling/simulation seem to display features of surrogate reasoning (Swoyer 1991), which is visible, for instance, when one experiments with model organisms instead of the actual organisms of interest. Consequently, the relationship of a model or experiment to its respective target need not distinguish the two activities from each other. Peschard (2013) disagrees, however; she suggests that one should pay attention to the kinds of “target systems” that simulation and experimentation pick, respectively, when they are used side by side in scientific research. According to her, the target system of the simulation is the system represented by the manipulated model: “it is the system that simulation is designed to produce information about” (see also Giere 2009). In the case of experimentation, the target system is the experimental system, for example, the model organism. The experimental results concern the interventions on the model organism (e.g., rats), although the eventual epistemic motivation might be to gain information on the influence of a certain drug in humans.
Peschard’s argument hints at the fact that at the level of scientific practice we often do not have any difficulties in distinguishing model systems from experimental systems, although borderline cases exist. Models and simulations are considered as kinds of representations even if they did not represent any real-world system but rather depicted a hypothetical or fictional system. The point is that being representations they typically are expressed in other media than from what their targets are made of, whereas experimental objects are supposed to share at least partly the same material makeup as the systems scientists are primarily interested in.
Indeed, the right kind of materiality has been claimed to be the distinguishing mark of experiments and even the reason for their epistemic superiority to simulations. The idea is that the relationship between a simulation and its target is nevertheless abstract, whereas the relationship between an experimental system and its target is grounded in the same material being supposedly governed by the same kinds of causes (Guala 2002; Morgan 2003). Consequently, while in simulation one experiments with a (formal) representation of the target system, in experimentation the experimental and target systems are made of the “same stuff.” This difference also explains, according to Morgan and Guala, why experiments have more epistemic leverage than simulations. For example, anomalous experimental findings are more likely to incur change in our theoretical commitments than unexpected results from simulations (Morgan 2005).
Despite the intuitive appeal of the importance of the “same” materiality, it has been contested on different grounds. Morrison (2009) points out that even in the experimental contexts the causal connection with the physical systems of interest is often established via models (see, however, Giere 2009 for a counterargument). Consequently, materiality is not able to deliver an unequivocal epistemic standard that distinguishes simulation outputs from experimental results. Parker (2009) questions the alleged significance of the “same stuff.” She interprets the “same stuff” to mean, for instance, the same fluid and points out that in traditional laboratory experiments on fluid phenomena many other things such as the depth of the fluid and the size, shape, roughness, and movement of any container holding it may matter. This leads her to suggest that it is the “relevant similarities” that matter for the justified inferences about the phenomena. Let us note that this renders, once again, modeling and experimentation close to each other.
In trying to get a firmer grip on the experimental nature of modeling and to which extent this perspective on modeling draws modeling and experimentation closer to each other, we will in the next sections take an excursion into the study of genetic circuits in the emerging field of synthetic biology. We will focus on the relationship of mathematical models, experiments on model organisms, and synthetic models in circadian clock research, which provides one of the most studied gene regulatory systems. All three activities are used in close combination within this field to study how genetic circuits regulate the rhythmic behavior of cells. This combinational approach has been portrayed by synthetic biologists as the “synthetic biology paradigm” (Sprinzak and Elowitz 2005). In the rest of this essay we discuss the epistemic rationale of this paradigm, which we call “synthetic strategy,” and examine what it tells us about the characteristics of modeling and experimentation.
The Synthetic Strategy in the Study of Genetic Circuits
Synthetic biology is a novel and highly interdisciplinary field located at the interface of engineering, physics, biology, chemistry, and mathematics. It developed along two main, though interdependent, paths: the engineering of novel biological components and systems, and the use of synthetic gene regulatory networks to gain understanding on the basic design principles underlying specific biological functions, such as the circadian clock. A particular modeling strategy, combinational modeling, is one of the distinctive features of the basic science approach to synthetic biology. It consists of a combinational use of model organisms, mathematical models, and synthetic models.
The basic idea of this combinational modeling strategy is shown in Figure 4.1, which is taken from a review article by Sprinzak and Elowitz (2005). The two authors call this approach “the synthetic biology paradigm.” The diagram indicates two important differences between the natural and the synthetic genetic circuits (i.e., synthetic models):
- 1. The natural circuit exhibits a much higher degree of complexity than the synthetic circuit.
- 2. The synthetic circuit has been designed by using different genes and proteins than the natural circadian clock circuit.
Consequently, synthetic models have the advantage of being less complex than model organisms. On the other hand, in comparison with mathematical models they are of “the same materiality” as their biological counterparts, naturally evolved gene regulatory networks. That is, they consist of the same kind of interacting biochemical components and are embedded in a natural cell environment. This same materiality is crucial for the epistemic value of synthetic models: they are expected to operate in the same way as biological systems although the biochemical components are organized in a novel configuration.

Figure 4.1. The “synthetic biology paradigm” according to Sprinzak and Elowitz (2005). The upper part of the diagram depicts the combinational modeling typical of synthetic strategy, and the lower part compares our present understanding of the circadian clock circuit of the fruit fly (Drosophila melanogaster) with a synthetic genetic circuit, the Repressilator.
In what follows, we argue that the combinational synthetic strategy arose in response to the constraints of mathematical modeling, on the one hand, and experimentation with model organisms on the other hand. There seemed to remain a gap between what could be studied mathematically and what scientists were able to establish experimentally. In particular, the experiments could not give any conclusive answer as to whether the hypothetical mechanisms that were suggested by mathematical models could be implemented as molecular mechanisms capable of physically generating oscillatory phenomena like the circadian rhythm. The problem was that in the experiments on model organisms such as Drosophila many genes and proteins underlying the circadian clock were found but the dynamics of their interaction regulating the day and night rhythm remained largely inaccessible. In consequence, the mechanism and dynamics suggested by mathematical models were probed by constructing synthetic models whose design was based on mathematical models and their simulations.
In the next sections, we will discuss in more detail the respective characteristics and specific constraints of mathematical modeling and the experimentation that gave rise to synthetic modeling. We start from mathematical modeling, which predated the experimental work in this area. Our discussion is based on one of the most basic models of gene regulation because it helps us to highlight some characteristic features of mathematical modeling that are less visible in subsequent models. Also, in pioneering works authors are usually more explicit about their modeling choices, and this certainly applies to Brian Goodwin’s Temporal Organization in Cells (1963).
Mathematical Modeling
In Temporal Organization in Cells (1963) Brian Goodwin introduced one of the earliest and most influential mathematical models of the genetic circuit underlying the circadian rhythm. This book is an example of an attempt to apply concepts from engineering and physics to biology. Inspired by Jacob and Monod’s (1961) operon model of gene regulation, Goodwin explored the mechanism underlying the temporal organization in biological systems, such as circadian rhythms, in terms of a negative feedback system. Another source of inspiration for him was the work of the physicist Edward Kerner (1957). Kerner had tried to formulate a statistical mechanics for the Lotka–Volterra model, which then prompted Goodwin to attempt to introduce a statistical mechanics for biological systems. These aims created the partly competing constraints of the design of Goodwin’s model, both shaping its actual formulation and the way it was supposed to be understood. A third constraint was due to limitations of the mathematical tools for dealing with nonlinear dynamics. These three constraints are different in character. The first constraint was largely conceptual, but it had mathematical implications: the idea of a negative feedback mechanism that was borrowed from engineering provided the conceptual framework for Goodwin’s work. It guided his conception of the possible mechanism and its mathematical form.
The second constraint, due primarily to the attempt to formulate a general theory according to the example provided by physics, was based on the assumption that biological systems should follow the basic laws of statistical mechanics. Goodwin described his approach in the following way: “The procedure of the present study is to discover conservation laws or invariants for a particular class of biochemical control systems, to construct a statistical mechanics for such a system, and to investigate the macroscopic behavior of the system in terms of variables of state analogous to those of physics: energy, temperature, entropy, free energy, etc.” (1963, 7). This procedure provided a course of action but also imposed particular constraints such as the restriction to conservative systems, although biological systems are nonconservative as they exchange energy with the environment. We call this particular constraint, deriving from the goal of formulating a statistical mechanics for biological systems, a fundamental theory constraint. The third set of constraints was mathematical in character and related to the nature of the mathematical and computational methods used in the formulation of the model. Because of the nonlinearity introduced by the negative feedback loop, the tractability of the equations of the model posed a serious challenge.
The three types of constraints—conceptual, fundamental, and mathematical—characterize the theoretical toolbox available for mathematically modeling a specific system. But as a hammer reaches its limits when used as a screwdriver, the engineering concepts and especially the ideal of statistical mechanical explanation proved problematical when applied to biological systems. Indeed, in later systems and synthetic biology the aim for a statistical mechanics for biological systems was replaced by the search for possible design principles in biological systems. The concept of the negative feedback mechanism was preserved, functioning as a cornerstone for subsequent research, but there was still some uneasiness about it that eventually motivated the construction of synthetic models.
The toolbox-related constraints should be distinguished from the constraints more directly related to the biological systems to be modeled. These constraints are due to the enormously complex behavior of biological systems, which, as we will show, plays an important yet different role in mathematical modeling, experimentation, and synthetic modeling, respectively. Obviously the tool-related constraints are not static. Mathematical and computational methods develop, and theoretical concepts can change their meaning especially in interdisciplinary research contexts such as synthetic biology. Furthermore, the constraints are interdependent, and the task of a modeler consists in finding the right balance between them. We will exemplify these points by taking a closer look into the Goodwin model.
The basic structure of the network underlying the molecular mechanism of Goodwin’s model of temporal organization is represented in Figure 4.2. The main structure of the model is rather simple, consisting of a negative feedback loop. It consists of a genetic locus Li, synthesizing messenger RNA (mRNA) in quantities represented by the variable Xi. The mRNA leaves the nucleus and enters the ribosome, which reads out the information from the mRNA and synthesizes proteins in quantities denoted by Yi. The proteins are connected to metabolic processes. At the cellular locus C the proteins influence a metabolic state, for example, by enzyme action, which results in the production of metabolic species in quantity Mi. A fraction of the metabolic species is traveling back to the genetic locus Li where it represses the expression of the gene.

Figure 4.2. The circuit diagram underlying the Goodwin model (1963, 6).
This mechanism leads to oscillations in the protein level Yi regulating temporal processes in the cell, such as the circadian rhythm. Goodwin described the mechanism by a set of coupled differential equations, which are nonlinear due to the feedback mechanism. The differential equations are of the following form:
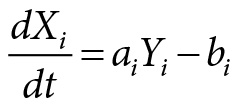
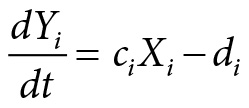
where aiYi describes the rate of mRNA controlled by the proteins synthetized and bi its degradation. In the same way ciXi describes the synthesis of the protein and di its degradation. The set of kinetic equations describes a deterministic dynamics.
In formulating his model, Goodwin had to make simplifying assumptions through which he attempted to deal with two important constraints: the complexity of the system consisting of a variety of biochemical components and processes, and the complexity due to the nonlinear dynamics of the assumed mechanism. First, he had to leave aside many known biochemical features of the circadian clock mechanism, and, second, he had to make assumptions that would allow him to simplify the mathematical model in such a way that he could use numerical methods to explore its complex dynamic behavior without having to solve the nonlinear coupled differential equations.
Goodwin was able to show by performing very basic computer simulations that the changes in the concentrations of mRNA and proteins form a closed trajectory. This means that the model system is able to perform regular oscillations, like those exhibited by circadian rhythms—but for the wrong reasons. Goodwin wrote, “The oscillations which have been demonstrated to occur in the dynamic system . . . persist only because of the absence of damping terms. This is characteristic of the behavior of conservative (integrable) systems, and it is associated with what has been called weak stability” (1963, 53). He went on to explain that a limit-cycle dynamics would have been the desirable dynamic behavior with respect to biological organisms. In this case, after small disturbances, the system moves back to its original trajectory—a characteristic of open (nonconservative) systems. But conceiving biological systems as open systems would have required the use of nonequilibrium statistical mechanics, which would have meant giving up some mathematical advantages of treating them as closed systems. Consequently, to simultaneously fulfill the aim of modeling a mechanism that produces oscillatory behavior and the aim to formulate a statistical mechanics for biological systems, Goodwin ended up presenting a model that he believed could only approximate the behavior he suspected to actually be taking place.
Even though Goodwin’s model was not a complete success, it nevertheless provided a basic template for studying periodic biological phenomena at the molecular level. The subsequent modeling efforts were built on it, although in those endeavors the aim of formulating a statistical mechanics for biological systems was left behind. Instead, the notion of a feedback mechanism was made the centerpiece, the main constraints of the modeling approach now being the mathematical difficulties due to the nonlinear, coupled differential equations and the related problem of tractability. This meant that only some components and biochemical processes in natural systems could be taken into account. However, the subsequent models became more detailed as the first experiments exploring the molecular basis of the circadian rhythms became possible in the mid-1970s. These experiments, as we will show later, came with their very own constraints. Although modelers were able to partly bracket the complexity of biological systems by simply ignoring most of it, this was not possible in the experimental work.
Experimentation
During the 1960s the American biologist Colin Pittendrigh developed special methods and instruments that would allow him to study the circadian rhythms in rest and activity behavior and the eclosion of the fruit fly, Drosophila melanogaster (Pittendrigh 1954). Drosophila seemed to provide a good model organism for the study of the circadian rhythm. Take, for example, the eclosion. Drosophila goes through four different larva stages. At the end of the fourth larval stage the larva crawls into the soil and pupates. It takes the larva seven days to transform into a fly. When it emerges from the soil the outer layer of its body has to harden. At this stage the fly runs the risk of drying out. Because of this, its emergence from the soil should take place early in the morning when the air is still moist. Pittendrigh showed that the eclosion rhythm does not depend on any external cues such as light or temperature, and he reasoned that an endogenous mechanism—the circadian clock—is controlling the emergence of Drosophila from its pupa stage. Pittendrigh’s studies provided the impetus for experiments in which scientists targeted the genes and mechanism underlying the circadian clock.
There were also other reasons for why Drosophila seemed to be the model organism of choice in isolating the genes contributing to the circadian clock. Before scientists started to use Drosophila in circadian clock research, it had already been extensively studied in genetics (see Kohler 1994). Drosophila breeds cheaply and reproduces quickly. Another important reason is its genetic tractability. The early genetic work suggested that the genome of the Drosophila contained only around 5,000 or 6,000 genes, no more than many bacteria. A further important incentive for choosing Drosophila is the size of its chromosomes. The salivary gland of the fruit fly contains giant chromosomes that can easily be studied under the microscope (see Morange 1998). Thus, when scientists started the investigation of the genetic makeup of the circadian clock, they had already at their disposal a lot of the experience and expertise from Drosophila genetics.
The first circadian clock gene of the Drosophila was found by Ronald Konopka and Seymour Benzer at the beginnings of the 1970s. They named the gene period (per) because the mutants showed a drastic change in their normal 24-hour rhythm (Konopka and Benzer 1971). In their experiments Konopka and Benzer produced mutants by feeding chemicals to the flies. The two scientists were especially interested in flies that showed changes in their eclosion rhythm. The critical point of these experiments consisted of linking the deviation in the timing of the eclosion to the genetic makeup of the fly. In this task Konopka and Benzer crossed male flies with a rhythm mutation with females carrying visible markers. The female and male off-springs were mated again. The recombination of the genetic material in the mothers led to various recombinants for the rhythm mutation. The visible markers made it possible to locate genes linked to the circadian clock and to identify the first circadian clock gene period (per).
The experimental research on circadian rhythms in molecular biology and genetics progressed slowly after Konopka and Benzer published their results. In the mid-1980s and early 1990s the situation started to change because of the further advances in molecular biology and genetics, such as transgenic and gene knockout technologies. The transgenic methods make use of recombinant DNA techniques to insert a foreign gene into the genome of an organism, thus introducing new characters into it that were not present previously. Gene knockout technologies in turn inactivate specific genes within an organism and determine the effect this has on the functioning of the organism. As a result, more genes, proteins, and possible mechanisms were discovered (see Bechtel 2011). However, despite the success of this experimental research program, the circadian clock research soon faced new challenges as attention started to shift from isolating the clock genes and their interrelations to the dynamics of these gene regulatory networks. To be sure, the theoretical concepts already studied by the mathematical modeling approach, such as negative and positive feedback, had informed researchers in the piecemeal experimental work of identifying possible gene regulatory mechanisms. For example, in mutation experiments different possible mechanisms were tried out by varying the experimental parameters in systematic ways, and the results were related to such feedback mechanisms that could account for the observed behavior.
Although the experimental strategy in circadian clock research has thus been very successful, it nevertheless has important constraints. First, there are technical constraints related to the available methods from molecular biology and genetics—such as creating the mutations and measuring the effects of the mutations. As already noted, the relaxation of some of these constraints led to the experimental approach that flourished from the mid-1980s onward. But even when it is possible to single out an explanatory mechanism experimentally, due to the complexity of biological systems there always remains the haunting question of whether all the components and their interactions have been found—whether the network is complete. This is a typical problem of the bottom-up experimental approach in molecular biology.
Another vexing question is whether the hypothetical mechanisms that researchers have proposed are the only ones that could explain the observations—which amounts to the traditional problem of underdetermination (which also besets the mathematical modeling approach to an even larger degree). But the most crucial constraint on the experimental approach—especially owing to the realization of the importance of the interaction between different genes and proteins—is the insufficient means of the experimental approach to study the dynamics. The experiments do not allow direct, but only indirect, observation of the network architecture and dynamics. As we will see, a new kind of modeling approach—synthetic modeling—was developed to observe the dynamics of genetic networks within the cell. This new modeling practice raised further important questions: how gene regulatory networks like the circadian clock interact with the rest of the cell, and how stochastic fluctuations in the number of proteins within the cell influence the behavior of the clock.
Synthetic Modeling
Although mathematical modeling (and simulation) and experimentation informed each other in circadian clock research—mathematical modeling suggesting possible mechanism designs, and experimentation in turn probing them and providing more biochemical detail—they still remained apart from each other. One important reason for this was that the modeling effort was based on rather schematic templates and related concepts, often originating from fields of inquiry other than biology. It was unclear whether biological organisms really functioned in the way the modelers suggested, even though the models were able to exhibit the kind of stable oscillations that were sought after.
The problem was twofold. First, the phenomena that the mathematical models were designed to account for could have been produced by other kinds of mechanisms. Second, and even more importantly, researchers were uncertain whether the general mechanisms suggested by mathematical models could be realized by biological organisms. The hybrid construction of synthetic models provides a way to deal with this problem. On the one hand, they are of the same materiality as natural gene regulatory networks because they are made of the same biological material, interacting genes and proteins. On the other hand, they differ from model organisms in that they are not the results of any evolutionary process, being instead designed on the basis of mathematical models. When engineering a synthetic model, a mathematical model is used as a kind of blueprint: it specifies the structure and dynamics giving rise to particular functions. Thus, the synthetic model has its origin in the mathematical model, but it is not bound by the same constraints. The model is constructed from the same material as the biological genetic networks, and it even works in the cell environment. Consequently, even if the synthetic model is not understood in all its details, it provides a simulation device of the same kind as its naturally evolved counterparts.
The Repressilator
The Repressilator, an oscillatory genetic network, is one of the first and most famous synthetic models. It was introduced in 2000 by Michael Elowitz and Stanislas Leibler (2000). In an interview Michael Elowitz explained the basic motivation for constructing it:
I was reading a lot of biology papers. And often what happens in those papers is that people do a set of experiments and they infer a set of regulatory interactions, and . . . at the end of the paper is a model, which tries to put together those regulatory interactions into a kind of cartoon with a bunch of arrows saying who is regulating who . . . And I think one of the frustrations . . . with those papers was [I was] always wondering whether indeed that particular configuration of arrows, that particular circuit diagram really was sufficient to produce the kinds of behaviors that were being studied. In other words, even if you infer that there’s this arrow and the other arrow, how do you know that that set of arrows is actually . . . working that way in the organism. (Emphasis added)
Elowitz underlines in this quote the importance of studying the dynamics of network behavior, for which both mathematical and synthetic modeling provide apt tools. However, even though mathematical models can imitate the dynamics of biological phenomena, it is difficult to tell whether the kinds of networks that mathematical models depict really are implemented by nature. This is addressed by synthetic modeling.
From the perspective of the experimental features of modeling, it is important to notice how in the following statement Elowitz simultaneously portrays synthetic circuits as experiments and as a way of studying the general features of genetic circuits:
It seemed like what we really wanted to do is to build these circuits to see what they really are doing inside the cell . . . That would be in a way the best test of it . . . of what kind of circuits were sufficient for a particular function. (Emphasis added).
The first step in constructing the Repressilator consisted in designing a mathematical model, which was used to explore the known basic biochemical parameters and their interactions. Next, having constructed a mathematical model of a gene regulatory network, Elowitz and Leibler performed computer simulations on the basis of the model. They showed that there were two possible types of solutions: “The system may converge toward a stable steady state, or the steady state may become unstable, leading to sustained limit-cycle oscillations” (Elowitz and Leibler 2000, 336). Furthermore, the numerical analysis of the model gave insights into the experimental parameters relevant for constructing the synthetic model and helped in choosing the three genes used in the design of the network.
The mathematical model functioned as a blueprint for engineering the biological system. The mathematical model is of the following form:
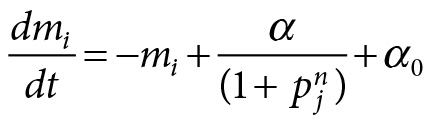
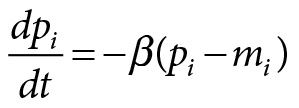
with

In this set of equations, pi is the concentration of the proteins suppressing the function of the neighbor genes, and mi (where i is lacI, tetR, or cl) is the corresponding concentration of mRNA. All in all, there are six molecule species (three proteins functioning as repressors and three genes) all taking part in transcription, translation, and degradation reactions.
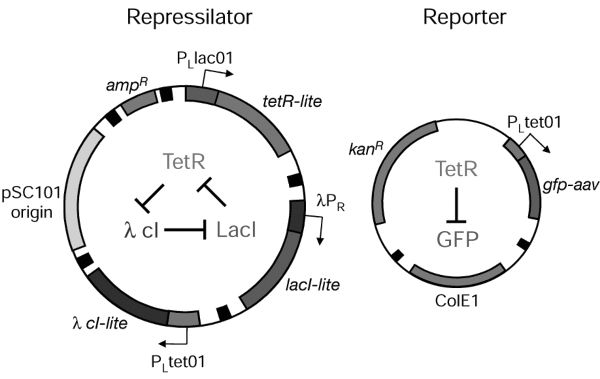
Figure 4.3. The main components of the Repressilator (left side) and the Reporter (right side). (Source: Elowitz and Leibler 2000, 336).
In Figure 4.3 the synthetic genetic regulatory network, the Repressilator, is shown on the left side and consists of two parts. The outer part is an illustration of the plasmid constructed by Elowitz and Leibler. The plasmid is an extrachromosomal DNA molecule integrating the three genes of the Repressilator. Plasmids occur naturally in bacteria. They can replicate independently, and in nature they carry genes that may enable the organism to survive, such as genes for antibiotic resistance. In the state of competence, bacteria are able to take up extrachromosomal DNA from the environment. In the case of the Repressilator, this property allowed the integration of the specific designed plasmid into Escherichia coli bacteria. The inner part of the illustration represents the dynamics between the three genes, TetR, LacI, and λcl. The three genes are connected by a negative feedback loop. This network design is directly taken from engineering, although the construction of it from molecular parts is a remarkable (bio)technological feat. Within electrical engineering this network design is known as the ring oscillator.
The left side of the diagram shows the Reporter consisting of a gene expressing green fluorescent protein (GFP), which is fused to one of the three genes of the Repressilator. The GFP oscillations in the protein level make visible the behavior of transformed cells, allowing researchers to study them over time by using fluorescence microscopy. This was quite epoch making as it enabled researchers to study the behavior of individual living cells. Green fluorescent proteins have been known since the 1960s but their utility as tools for molecular biology was recognized first in the 1990s, and several mutants of GFP were developed.[4] Apart from GFPs and plasmids, there were other important methods and technologies such as polymerase chain reaction (PCR) that enabled the construction of synthetic genetic circuits (Knuuttila and Loettgers 2013b).[5]
The Repressilator had only limited success. It was able to produce oscillations at the protein level, but these showed irregularities. From the perspective of the interplay of mathematical and synthetic modeling, the next move made by Elowitz and Leibler seems crucial: to find out what was causing such noisy behavior they reverted back to mathematical modeling. In designing the Repressilator, Elowitz and Leibler had used a deterministic model. A deterministic model does not take into account stochastic effects such as stochastic fluctuations in gene expression. Performing computer simulations on a stochastic version of the original mathematical model, Elowitz and Leibler were able to reproduce similar variations in the oscillations as observed in the synthetic model. This led researchers to conclude that stochastic effects may play a role in gene regulation—which gave rise to a new research program that targeted the role of noise in biological organization. This new research program revived the older discussions on nongenetic variation (e.g., Spudich and Koshland 1976), but this time the new tools such as GFP and synthetic modeling enabled researchers to observe nongenetic variation at an intracellular level. The researchers of the Elowitz Lab were especially interested in studying the various sources of noise in individual cells and the question of whether noise could be functional for living cells (e.g. Elowitz et al. 2002; Swain, Elowitz, and Siggia 2002).
The Dual-Feedback Synthetic Oscillator
The work of Jeff Hasty and his coworkers at University of California–San Diego provides another good example of how the combination of mathematical and synthetic modeling can lead to new insights that mere mathematical modeling (coupled with experimentation with model organisms) cannot provide. They constructed a dual-feedback synthetic oscillator exhibiting coupled positive and negative feedback, in which a promoter drives the production of both its own activator and repressor (Stricker et al. 2008; Cookson, Tsimring, and Hasty 2009). The group introduced the synthetic oscillator by explaining how it was based on both experimental work on the Drosophila melanogaster clock and earlier theoretical work. The mathematical model providing the blueprint for the synthetic model was set forth by Hasty et al. (2002). This model, as Cookson et al. put it, was “theoretically capable of exhibiting periodic behavior” (Cookson, Tsimring, and Hasty 2009, 3932). Figure 4.4 shows the network diagram of the dual-feedback oscillator.
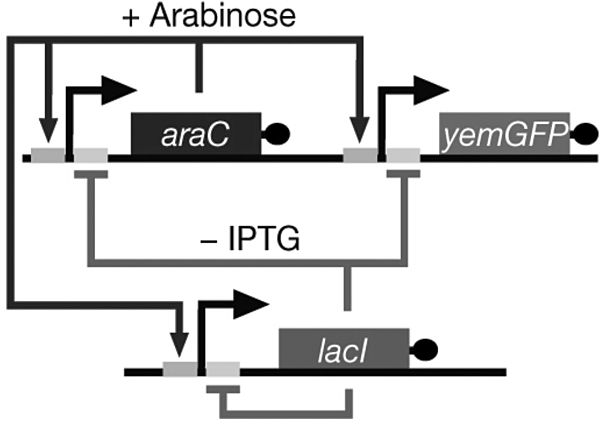
Figure 4.4. A diagrammatic representation of the dual-feedback oscillator (Source: Cookson, Tsimring, and Hasty 2009, 3934).
The synthetic network consists of two genes: araC and lacI. The hybrid promoter Plac/ara−1 (the two small adjacent boxes) drives transcription of araC and lacI, forming positive and negative feedback loops. It is activated by the AraC protein in the presence of arabinose and repressed by the LacI protein in the absence of isopropyl β-D-1-thiogalactopyranoside (IPTG). The oscillations of the synthetic system are made visible by a GFP. Like the Repressilator, this system provides a material system allowing for the study of the oscillatory dynamic of the dual-feedback system; the basic properties and conditions of the oscillatory dynamic can be estimated on the basis of the components of the model and their interactions. When arabinose and IPTG are added to the system, the promoter becomes activated, and the system’s two genes, araC and lacI, become transcribed. Increased production of the protein AraC in the presence of arabinose results in a positive feedback loop that increases the promoter activity. On the other hand, the increase in LacI production results in a linked negative feedback loop that decreases promoter activity. The difference in the promoter activities of the two feedback loops leads to the oscillatory behavior (Knuuttila & Loettgers 2013a, 2013b).
On the basis of the analysis of the dual-feedback oscillator, the researchers made several observations that were difficult to reconcile with the original mathematical model that had informed the construction of the synthetic model. The most surprising finding concerned the robustness of the oscillations. Whereas the mathematical model predicted robust oscillations only for a restricted set of parameters, the synthetic model instead showed robust oscillations for a much larger set of parameter values! The researchers were perplexed by the fact that “it was difficult to find inducer levels at which the system did not oscillate” (Cookson, Tsimring, and Hasty 2009, 3934, italics in original). They had anticipated that they would need to tune the synthetic model very carefully for it to yield oscillations, as the analysis of the mathematical model had shown that there was only a very small region in the parameter space where it would oscillate.
These contradictory results led the researchers in question to reconsider the original model. Cookson, Tsimring, and Hasty wrote about this as follows: “In other words, it became increasingly clear that the observed oscillations did not necessarily validate the model, even though the model predicted oscillations. We were able to resolve the discrepancy between the model and theory by reevaluating the assumptions that led to the derivation of the model equations” (2009, 3934). This statement does not reveal how laborious the actual modeling process was—it took a whole year. In the beginning the researchers had no clue how to account for the too-good performance of the model, or as the leader of the laboratory, Jeff Hasty, put it in an interview: “We did not understand why it was oscillating even though we designed it to oscillate.” So he suggested to one of the postdoctoral researchers in the laboratory (“a modeling guy”) an unusual way to proceed:
We have sort of physicists’ mentality: we like simple models. But [I thought that] maybe in this case we should start with just some big model where we model more of the interactions, and not try to simplify it into something eloquent . . . And, my postdoc was a bit reluctant because we did not know . . . many of the parameters, in anything we were doing . . . So he said: “What’s the point of that?” . . . But my reasoning was, well, it should be robustly oscillating, so it should not really matter what the parameters are. You should see oscillations all over the place.[6]
With the bigger model the researchers were indeed able to create very robust oscillations. But the new problem was that “the big model was not necessarily telling us more than the big experiment.”
However, when the researchers started to look at the time series of the model they found out that a small time delay in the negative feedback loop caused by a cascade of cellular processes was crucial for producing robust oscillations. Another unexpected finding concerned the enzymatic decay process of the proteins that turned out to be crucial for the sustained oscillations. The limited availability of the degradation machinery provided by the cell improved the precision of the oscillator by causing an indirect posttranslational coupling between the activator (AraC) and repressor (LacI) proteins.[7] As such, this was a consequence of an unintended interaction with the host cell that showed that interactions with the cell environment can be advantageous for the functioning of synthetic circuits (for more details, see Knuuttila and Loettgers 2013a, 2013b). This is as remarkable an insight as the one concerning the functional role of noise, given that the original program of synthetic biology was based on the idea of constructing modular synthetic circuits from well-characterized components. Other researchers in the field of synthetic biology were quick to pick up the findings of Hasty and his coworkers, suggesting strategies to develop next-generation synthetic models that would integrate more closely with the endogenous cellular processes of the host organisms (Nandagopal and Elowitz 2011).
In conclusion, synthetic models such as the Repressilator and the dual-feedback oscillator have so far been limited to simple networks that are designed in view of what would be optimal for the behavior under study. This means that such networks need not be part of any naturally occurring system; they are chosen and tuned on the basis of the simulations of the underlying mathematical model and other background knowledge in such a way that the resulting mechanism would allow for (stable) oscillations. These technical constraints imply a constraint on what can be explored by such synthetic models: possible design principles in biological systems. Synthetic models are thus like mathematical models, but they take one step closer to empirical reality in showing that the theoretical mechanism in question is actually realizable in biological systems.
How to Understand the Experimental Character of Modeling?
In the previous sections we studied the synthetic strategy in the study of genetic circuits, which is based on a close triangulation of experiments and mathematical and synthetic models. We have shown, in particular, how synthetic models have generated new theoretical insights as a result of their mismatch with the original mathematical models that provided the blueprints for their construction. As synthetic modeling involves a step toward materially embodied experimental systems, it seems instructive to study the philosophical discussion on modeling and experimentation through this case. In the second section we discussed two arguments for seeing models as kinds of experiments.
The argument from isolation draws an analogy to experimental practice in claiming that models are abstracted from real-world systems through suitable assumptions in order to study how a causal factor operates on its own. This does not suit the experimental practice of synthetic biology for reasons that seem to us applicable to many other modeling practices as well. First, instead of targeting the influence of isolated causal factors, the modelers in the field of systems and synthetic biology focus on the interaction of the (molecular) components of the assumed mechanism. What is at stake is whether the kinds of feedback loops that have extensively been studied in physics and engineering could generate the periodic/oscillatory behavior typical of biological systems. The issue is of great importance: in human engineered systems oscillations are predominantly a nuisance, but in biological systems they comprise one of the very ways through which they regulate themselves (Knuuttila and Loettgers 2013a, 2014). This was already pointed out by Brian Goodwin, who studied, in addition to circadian clocks, other biological feedback mechanisms such as metabolic cycles (Goodwin 1963).
William Bechtel and Adele Abrahamsen have argued, on the basis of a meticulous study of circadian clock research, that models provide dynamic mechanistic explanations. The idea is that while the experimental work typically aims to discover the basic components and operations of biological mechanisms (i.e., genes and associated proteins) the task of modeling is to study their organization and “dynamical orchestration” in time (e.g., Bechtel 2011; Bechtel and Abrahamsen 2011).[8] More generally, mathematical models in many sciences can be understood as systems of interdependencies, whose outcomes over time are studied by modeling. The reason mathematical modeling provides such an indispensable tool for science is that a human mind cannot track the interaction of several variables—and when it comes to nonlinear dynamics typical of feedback loops, computer simulations are needed even in the case of such simple systems as the Lotka–Volterra equations (Knuuttila and Loettgers 2012).
One conceivable way to rescue the idea of isolation would be to reformulate it in such a way that the focus is not on the behavior and outcomes of isolated causal factors but on isolating a mechanism instead. As synthetic biologists try to uncover what they call “the basic design principles” of biological organization, this argument may seem initially plausible. Yet from the perspective of the actual modeling heuristic of synthetic biology, it is questionable whether the idea of isolating a mechanism has any more than metaphorical force. As most of the biochemical details of the systems studied are unknown, the modeling process in this field cannot be understood as isolating a possible mechanism from empirically known components and their interactions.
As one of the pioneers of synthetic modeling described his situation at the end of 1990s, “I did not know what equations to write down. There was really not any literature that would guide me.”[9] The modeling process that ensued from the surprisingly robust oscillations of the dual-feedback oscillator provides a nice example of this difficulty. Even though the researchers tried to add details to their original model, it did not recapitulate what they saw happening in their synthetic model. Only through using a larger, partly speculative model were the researchers able to arrive at some hypotheses guiding the consequent model building. Thus, the modeling process was more hypothetical in nature than it would have been had it primarily consisted of the abstracting of a mechanism from known empirical details—and then subsequently adding them back.
The other argument for treating models as experiments underlines the interventional dimension of modeling, which is especially clear in the case of computer simulations. In dealing with both computer simulations and experiments one usually intervenes in more complex and epistemically opaque systems than when one manipulates highly idealized, mathematically tractable models. Lenhard (2006) suggests that simulation methods produce “understanding by control,” which is geared toward design rules and predictions. This provides an interesting analogy between simulations and experiments on model organisms: in both of them one attempts through control to overcome the complexity barrier. Although living organisms are radically more complex than simulation models, this feature of theirs can also be turned into an epistemic advantage: if one experiments with living organisms instead of in silico representations of them, the assumedly same material offers a causal handle on their behavior, as Guala and Morgan suggested.
Waters (2012) has lucidly spelled out the advantages of using material experimental models by pointing out that this strategy “avoids having to understand the details of the complexity, not by assuming that complexity is irrelevant but by incorporating the complexity in the models.” We have seen how the epistemic rationale of synthetic modeling depends critically on this point. In constructing synthetic models from biological material and implementing them in the actual cell environment, researchers were able to discover new dimensions of the complex behavior of cells.
Yet synthetic models also go beyond the strategy of using model organisms in that they are more artificial, insofar as being novel, man-made biological entities and systems that are not the results of evolutionary processes. Aside from their use in developing useful applications, the artificial construction of synthetic models also can be utilized for theoretical purposes—and it makes them more akin to mathematical models than to experiments. Take the case of the Repressilator. It is less complex than any naturally occurring genetic circuit that produces circadian cyclic behavior. It is built of only three genes and a negative feedback loop between them. The three genes do not occur in such a constellation in any known genetic circuit, and even their order was carefully designed. Thus it was not supposed to imitate any natural circuit, but rather to identify the sufficient components and interactions of a mechanism able to produce a specific behavior, such as oscillations in protein levels. The components of the network were chosen to achieve the most optimal behavior, not to get as close as possible to any naturally evolved genetic network. This serves to show that what the researchers were after was to explore whether the various feedback systems studied in engineering and complex systems theory could create the kind of periodic self-regulatory behavior typical of biological organisms. Thus, synthetic modeling and mathematical modeling in biology are hypothesis-driven activities that seek to explore various theoretical possibilities.
It is important to note, however, that the model status of the Repressilator is not due to its being a model in the sense of being a representation of some real-world target system (cf. Weber 2012). It is difficult to see what it could be a model of, given its artificial constructed nature. It is rather a fiction—albeit a concrete one—made of biological material and implementing a theoretical mechanism. What makes it a model is its simplified, systemic, self-contained construction that is designed to explore certain pertinent theoretical questions. It is constructed in view of such questions and the outcomes or behavior that it is expected to exhibit. In this sense it is best conceived of as an intricate epistemic tool (for the notion of models as epistemic tools, see Knuuttila 2011).
In addition to the characteristics that synthetic circuits share with models, their specific epistemic value is due to the way these model-like features intertwine with their experimental nature. This is the reason why we consider the notion of an experimental model especially apt in the case of synthetic models. Several of the synthetic biologists we interviewed had a background in neurosciences, and they pointed out their dissatisfaction with the lack of empirical grounding in neuroscientific models. As discussed earlier, synthetic models are constructed to test whether the hypothetical mechanisms that were suggested by mathematical models could be implemented as molecular mechanisms capable of physically generating oscillatory molecular phenomena like the circadian rhythm. Thus, synthetic models derive their experimental empirical character from the fact that they are constructed from the same kinds of material components as their natural counterparts. They are best conceived of as engineered “natural” or “scientific kinds,” giving more control to the researchers of the system under study than the domesticated “natural kinds” (such as model organisms).
Moreover, by being implemented in a natural cell environment synthetic models are exposed to some further constraints of naturally evolved biological systems. Although these constraints are in general not known in all their details, the fact that they are there is considered particularly useful in the contexts in which one has an imperfect understanding of the causal mechanisms at work. This explains how the researchers reacted to the unexpected results. In the case of experimentation, anomalous or unexpected results are commonly taken more seriously than in modeling—if the model does not produce what is expected of it, modelers usually try to devise a better model. This was how the researchers also proceeded in the cases of the Repressilator and the dual-feedback oscillator. They went back to reconfigure their original mathematical models and even constructed new ones in the light of the behavior of synthetic models.
WE HAVE ARGUED through the case of synthetic modeling that although modeling and experimentation come close to each other in several respects, they nevertheless have some quite distinct features and uses. This explains why they typically are, in cases where it is possible, triangulated in actual scientific practices. Occasionally, from the combined effort of modeling and experimentation new hybrids are born—such as synthetic genetic circuits—that may properly be called experimental models. A closer analysis of the hybrid nature of synthetic models serves to show what is characteristic about modeling and experimentation, respectively.
Synthetic models share with mathematical models their highly simplified, self-contained construction, which makes them suitable for the exploration of various theoretical possibilities. Moreover, both mathematical models and synthetic models are valued for their systemic, dynamic features. On the other hand, synthetic models are like experiments in that they are expected to have the same material and causal makeup as the systems under study—which makes them more complex and opaque than mathematical models, yielding surprising, often counterintuitive results. This feature that synthetic models share with experiments typically requires mathematical modeling to find out what causes the behavior of synthetic circuits. The specific affordance of mathematical modeling in this task derives partly from its epistemic and quite literal “cheapness,” as mathematical models are fairly easy to set up and reconfigure in contrast to experiments. The recent modeling practice of synthetic biology shows rather conclusively how the triangulation of mathematical and synthetic modeling has led to new insights that otherwise would have been difficult to generate by either mathematical modeling or by way of experimentation on model organisms alone.
Notes
1. Genetic circuits are also called gene regulatory networks.
2. In addition to genetic circuits, synthetic biology also studies metabolic and signaling networks.
3. The interview material is from an interview with the synthetic biologist Michael Elowitz that was conducted in April 2010 by Andrea Loettgers.
4. Martin Chalfie, Osamu Shimomura, and Roger Y. Tsien shared the 2008 Nobel Prize in Chemistry for their work on green fluorescent proteins.
5. Polymerase chain reaction is a molecular biology technique originally introduced in 1983 that is now commonly used in medical and biological research laboratories to generate an exponentially increasing number of copies of a particular DNA sequence.
6. The interview material is from an interview with the synthetic biologist Jeff Hasty that was conducted in August 2013 by Tarja Knuuttila.
7. This limited availability of the degradation machinery led Hasty and his coworkers to study queuing theory in an attempt to mathematically model the enzymatic decay process in the cell (Mather et al. 2011).
8. For a partial critique, see Knuuttila and Loettgers 2013b. Bechtel and Abrahamsen assume in mechanist fashion that the experimentally decomposed components could be recomposed in modeling.
9. In such situations scientists often make use of model templates and concepts borrowed from other disciplines and subjects—in the case of synthetic biology, the modelers’ toolbox includes engineering concepts such as feedback systems and modeling methods from nonlinear dynamics (see the discussion in the chapter).
References
Barberousse, Anouk, Sara Franceschelli, and Cyrille Imbert. 2009. “Computer Simulations as Experiments.” Synthese 169: 557–74.
Bechtel, William. 2011. “Mechanism and Biological Explanation.” Philosophy of Science 78: 533–57.
Bechtel, William, and Adele Abrahamsen. 2011. “Complex Biological Mechanisms: Cyclic, Oscillatory, and Autonomous.” In Philosophy of Complex Systems, Handbook of the Philosophy of Science, vol. 10, edited by C. A. Hooker, 257–85. Oxford: Elsevier.
Cartwright, Nancy. 1999. “The Vanity of Rigour in Economics: Theoretical Models and Galilean Experiments.” Discussion Paper Series 43/99, Centre for Philosophy of Natural and Social Sciences, London School of Economics.
Cookson, Natalia A., Lev S. Tsimring, and Jeff Hasty. 2009. “The Pedestrian Watchmaker: Genetic Clocks from Engineered Oscillators.” FEBS Letters 583: 3931–37.
Elowitz, Michael B., and Stanislas Leibler. 2000. “A Synthetic Oscillatory Network of Transcriptional Regulators.” Nature 403: 335–38.
Elowitz, Michael B., Arnold J. Levine, Eric D. Siggia, and Peter S. Swain. 2002. “Stochastic Gene Expression in a Single Cell.” Science 297: 1183–86.
Giere, Ronald N. 2009. “Is Computer Simulation Changing the Face of Experimentation?” Philosophical Studies 143: 59–62.
Gilbert, Nigel, and Klaus Troitzsch. 1999. Simulation for the Social Scientists. Philadelphia: Open University Press.
Goodwin, Brian C. 1963. Temporal Organization in Cells: A Dynamic Theory of Cellular Control Processes. New York: Academic Press.
Guala, Francesco. 2002. “Models, Simulations, and Experiments.” In Model-Based Reasoning: Science, Technology, Values, edited by L. Magnani and N. Nersessian, 59–74. New York: Kluwer.
Hasty, Jeff, Milos Dolnik, Vivi Rottschäfer, and James J. Collins. 2002. “Synthetic Gene Network for Entraining and Amplifying Cellular Oscillations.” Physical Review Letters 88: 148101.
Humphreys, Paul. 2004. Extending Ourselves: Computational Science, Empiricism, and Scientific Method. Oxford: Oxford University Press.
Jacob, François, and Jacques Monod. 1961. “Genetic Regulatory Mechanisms in the Synthesis of Proteins.” Journal of Molecular Biology 3: 318–56.
Kerner, Edward H. 1957. “A Statistical Mechanics of Interacting Biological Species.” Bulletin of Mathematical Biophysics 19: 121–46.
Knuuttila, Tarja. 2011. “Modeling and Representing: An Artefactual Approach.” Studies in History and Philosophy of Science 42: 262–71.
Knuuttila, Tarja, and Andrea Loettgers. 2012. “The Productive Tension: Mechanisms vs. Templates in Modeling the Phenomena.” In Representations, Models, and Simulations, edited by P. Humphreys and C. Imbert, 3–24. New York: Routledge.
Knuuttila, Tarja, and Andrea Loettgers. 2013a. “Basic Science through Engineering: Synthetic Modeling and the Idea of Biology-Inspired Engineering.” Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences 44: 158–69.
Knuuttila, Tarja, and Andrea Loettgers. 2013b. “Synthetic Modeling and the Mechanistic Account: Material Recombination and Beyond.” Philosophy of Science 80: 874–85.
Knuuttila, Tarja, and Andrea Loettgers. 2014. “Varieties of Noise: Analogical Reasoning in Synthetic Biology.” Studies in History and Philosophy of Science Part A 48: 76–88.
Knuuttila, Tarja, and Andrea Loettgers. 2016a. “Modelling as Indirect Representation? The Lotka–Volterra Model Revisited.” British Journal for the Philosophy of Science 68: 1007–36.
Knuuttila, Tarja, and Andrea Loettgers. 2016b. “Model Templates within and between Disciplines: From Magnets to Gases—and Socio-economic Systems.” European Journal for Philosophy of Science 6: 377–400.
Kohler, E. Robert. 1994. Lords of the Fly: Drosophila Genetics and the Experimental Life. Chicago: University of Chicago Press.
Konopka, Ronald J., and Seymor Benzer. 1971. “Clock Mutants of Drosophila melanogaster.” Proceedings of the National Academy of Sciences of the United States of America 68: 2112–16.
Lenhard, Johannes. 2006. “Surprised by Nanowire: Simulation, Control, and Understanding.” Philosophy of Science 73: 605–16.
Lenhard, Johannes. 2007. “Computer Simulation: The Cooperation between Experimenting and Modeling.” Philosophy of Science 74: 176–94.
Mäki, Uskali. 1992. “On the Method of Isolation in Economics.” Poznań Studies in the Philosophy of Science and Humanities 26: 316–51.
Mäki, Uskali. 2005. “Models Are Experiments, Experiments Are Models.” Journal of Economic Methodology 12: 303–15.
Mather, W. H., J. Hasty, L. S. Tsimrig, and R. J. Williams. 2011. “Factorized Time-Dependent Distributions for Certain Multiclass Queueing Networks and an Application to Enzymatic Processing Networks.” Queuing Systems 69: 313–28.
Morange, Michel. 1998. A History of Molecular Biology. Cambridge, Mass.: Harvard University Press.
Morgan, Mary S. 2003. “Experiments without Material Intervention: Model Experiments, Virtual Experiments and Virtually Experiments.” In The Philosophy of Scientific Experimentation, edited by H. Radder, 216–35. Pittsburgh: University of Pittsburgh Press.
Morgan, Mary S. 2005. “Experiments versus Models: New Phenomena, Inference and Surprise.” Journal of Economic Methodology 12: 317–29.
Morrison, Margaret. 2008. “Fictions, Representations, and Reality.” In Fictions in Science: Philosophical Essays on Modeling and Idealization, edited by M. Suárez, 110–35. New York: Routledge.
Morrison, Margaret. 2009. “Models, Measurement and Computer Simulations: The Changing Face of Experimentation.” Philosophical Studies 143: 33–57.
Nandagopal, Nagarajan, and Michael B. Elowitz. 2011. “Synthetic Biology: Integrated Gene Circuits.” Science 333: 1244–48.
Parker, Wendy. 2009. “Does Matter Really Matter? Computer Simulations, Experiments and Materiality.” Synthese 169: 483–96.
Peschard, Isabelle. 2012. “Forging Model/World Relations: Relevance and Reliability.” Philosophy of Science 79: 749–60.
Peschard, Isabelle. 2013. “Les Simulations sont-elles de réels substituts de l’expérience?” In Modéliser & simuler: Epistémologies et pratiques de la modélisation et de la simulation, edited by Franck Varenne and Marc Siberstein, 145–70. Paris: Editions Materiologiques.
Pittendrigh, Collin. 1954. “On Temperature Independence in the Clock System Controlling Emergence Time in Drosophila.” Proceedings of the National Academy of Sciences of the United States of America 40: 1018–29.
Sprinzak, David, and Michael B. Elowitz. 2005. “Reconstruction of Genetic Circuits.” Nature 438: 443–38.
Spudich, J. L., and D. E. Koshland. 1976. “Non-Genetic Individuality: Chance in the Single Cell.” Nature 262: 467–71.
Stricker, Jesse, Scott Cookson, Matthew R. Bennet, William H. Mather, Lev S. Tsimring, and Jeff Hasty. 2008. “A Fast, Robust and Tunable Synthetic Gene Oscillator.” Nature 456: 516–19.
Swain, Peter S., Michael B. Elowitz, and Eric D. Siggia. 2002. “Intrinsic and Extrinsic Contributions to Stochasticity in Gene Expression.” Proceedings of the National Academy of Sciences of the United States of America 99: 12795–800.
Swoyer, Chris. 1991. “Structural Representation and Surrogative Reasoning.” Synthese 87: 449–508.
Waters, C. Kenneth. 2012. “Experimental Modeling as a Form of Theoretical Modeling.” Paper presented at the 23rd Annual Meeting of the Philosophy of Science Association, San Diego, Calif., November 15–17, 2012.
Weber, Marcel. 2012. “Experimental Modeling: Exemplification and Representation as Theorizing Strategies.” Paper presented at the 23rd Annual Meeting of the Philosophy of Science Association, San Diego, Calif., November 15–17, 2012.
Winsberg, Eric. 2003. “Simulated Experiments: Methodology for a Virtual World.” Philosophy of Science 70: 105–25.
Winsberg, Eric. 2009. “A Tale of Two Methods.” Synthese 169: 575–92.