2
Dynamics, Data, and Noise in the Cognitive Sciences
Anthony Chemero
Semi-Naïve Experimental Design
I have taught introductory laboratory psychology many times over the years. The psychology department at Franklin and Marshall College, where I taught this course regularly, is nearly unique in its commitment to teaching psychology as a laboratory science, and it is one of the very few institutions in the United States in which the first course in psychology is a laboratory course. It is a valuable experience for students, especially those who do not go on to major in a science, as it gives them a rudimentary understanding of hypothesis testing, experimental design, and statistics. It also reinforces for them that psychology really is an experimental science, having nothing to do with the fantasies of a famous Viennese physician. (Unfortunately, they mostly remember the rats.) The first meeting of the course stresses the very basic concepts of experimental design, and the lecture notes for that meeting include this sentence:
The goal of a good experiment is to maximize primary variance, eliminate secondary variance, and minimize error variance. (Franklin and Marshall Psychology Department 2012, 3)
This sentence, which I will henceforth call the methodological truism, requires some unpacking. Experiments in psychology look at the relationship between an independent variable (IV) and a dependent variable (DV). The experimenter manipulates the IV and looks for changes in measurements of the DV. Primary variance is systematic variance in the DV caused by the manipulations of the IV. Secondary variance is systematic variance in the DV caused by anything other than the manipulations of the IV. Error variance is unsystematic variance in the DV, or noise. The methodological truism, then, is the key principle of experimental design. A good experiment isolates a relationship between the IV and DV, and eliminates effects from other factors. Of course, although unsystematic variance in the DV is inevitable in our noisy world, it should be minimized to the extent possible. Because noise is inevitable, psychologists and other scientists tend to use some measure of the central tendency of the collection of measurements of the DV, such as the mean. This, in effect, washes out the unsystematic variance in the DV, separating the data from the noise.
Of course, the psychology department at Franklin and Marshall is not alone in teaching this material this way. You can find a version of the methodological truism in the textbook used for any introductory course in experimental methods. One of the claims I will argue for here is that the methodological truism is not, in general, true. I will argue for this point by describing experiments that use unsystematic variance in the DV as their most important data. That is, I will be calling into question the distinction between data and noise as these are understood in psychology and the cognitive sciences more broadly. To do this, I will need to describe how dynamical modeling works in the cognitive sciences and describe a set of experiments in my own laboratory as a case study in using noise as data. Along the way, I will grind various axes concerning dynamical models in the cognitive sciences as genuine explanations as opposed to “mere descriptions,” and concerning the role of dynamical models in the context of discovery.
Dynamical Modeling in the Cognitive Sciences
The research in the cognitive sciences that calls the methodological truism into question is a version of what is often called the dynamical systems approach to cognitive science (Kelso 1995; van Gelder 1995, 1998; Port and van Gelder 1996; Chemero 2009). In the dynamical systems approach, cognitive systems are taken to be dynamical systems, whose behavior is modeled using the branch of calculus known as dynamical systems theory. Dynamical modeling of the kind to be discussed later was introduced to psychology by Kugler, Kelso, and Turvey in 1980 as an attempt to make sense of Gibson’s claim in 1979 that human action was regular but not regulated by any homunculus. They suggested that human limbs in coordinated action could be understood as nonlinearly coupled oscillators whose coupling requires energy to maintain and so tends to dissipate after a time. This suggestion is the beginning of coordination dynamics, the most well-developed form of the dynamical systems modeling in cognitive science.
The oft-cited locus classicus for dynamical research is work from the 1930s by Erich von Holst (1935/1973; see Kugler and Turvey 1987, and Iverson and Thelen 1999 for good accounts). Von Holst studied the coordinated movements of the fins of swimming fish. He modeled the fins as coupled oscillators, which had been studied by physicists since the seventeenth century when Huygens described the “odd sympathy” of pendulum clocks against a common wall. Von Holst assumed that on its own a fin has a preferred frequency of oscillation. When coupled to another fin via the fish’s body and nervous systems, each fin tends to pull the other fin toward its preferred period of oscillation and will also tend to behave so as to maintain its own preferred period of oscillation. These are called the magnet effect and the maintenance effect, respectively. Von Holst observed that because of these interacting effects, pairs of fins on a single fish tended to reach a cooperative frequency of oscillation but with a high degree of variability around that frequency. One could model von Holst’s observations with the following coupled equations:
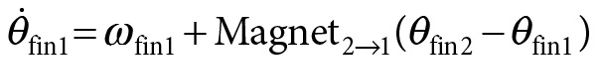
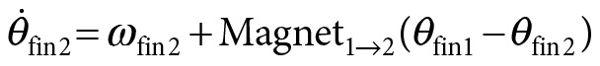
where ω is the preferred frequency of each fin and θ is the current frequency of each fin. In English, these equations say that the change in frequency of oscillation of each fin is a function of that fin’s preferred frequency and the magnet effect exerted on it by the other fin.
There are three things to note about these equations. First, the first and second terms in the equations represent the maintenance and magnet effects, respectively. Second, the equations are nonlinear and coupled. You cannot solve the first equation without solving the second one simultaneously, and vice versa. Third, with these equations you can model the behavior of the two-fin system with just one parameter: the strength of the coupling between the fins (i.e., the strength of the magnet effect).
This basic model is the foundation of later coordination dynamics, especially in its elaboration by Haken, Kelso, and Bunz (1985; see also Kugler, Kelso, and Turvey 1980). The Haken-Kelso-Bunz (HKB) model elaborates the von Holst model by including concepts from synergetics as a way to explain self-organizing patterns in human bimanual coordination. In earlier experiments, Kelso (1984) showed that human participants who were asked to wag the index fingers on both of their hands along with a metronone invariably wagged them in one of two patterns. Either they wagged the fingers in phase, with the same muscle groups in each hand performing the same movement at the same time, or out of phase, with the same muscle groups in each hand “taking turns.” Kelso found that out-of-phase movements were only stable at slower metronone frequencies; at higher rates, participants could not maintain out-of-phase coordination in their finger movements and transferred into in-phase movements. Haken, Kelso, and Bunz modeled this behavior using the following equation, a potential function
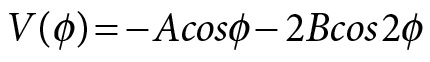
where φ is the relative phase of the oscillating fingers and V(φ) is the energy required to maintain relative phase φ. In-phase finger wagging has a relative phase of 0; out-of-phase finger wagging is relative phase π. The relative phase is a collective variable capturing the relationship between the motions of the two fingers. The transition from relative phase π to relative phase 0 at higher metronome frequencies is modeled by this derivative of relative phase:

In these equations the ratio B/A is a control parameter, a parameter for which quantitative changes to its value lead to qualitative changes in the overall system. These equations describe all the behavior of the system.
The behavior of the coordinated multilimb system can be seen from Figure 2.1, which shows the system potential at various values of the control parameter. At the top of the figure, when the metronome frequency is low and the control parameter value is near 1, there are two attractors: a deep one at ϕ = 0 and relatively shallow one at ϕ = ± π. As the value of the control parameter decreases (moving down the figure), the attractor at ±π gets shallower, until it disappears at 0.25. This is a critical point in the behavior system, a point at which qualitative behavior changes.
The HKB model accounts for the the behavior of this two-part coordinated system. Given the model’s basis in synergetics, it makes a series of other predictions about finger wagging, especially concerning system behavior around critical points in the system. All these predictions have been verified in further experiments. Moreover, the HKB model does not apply just to finger wagging. In the years since the original HKB study was published it has been extended many times and applied to a wide variety of phenomena in the cognitive sciences. That is, HKB has served as a guide to discovery (Chemero 2009) in that it has inspired a host of new testable hypotheses in the cognitive sciences. A brief survey of the contributions of the HKB model and its extensions to the cognitive and neurosciences would include the following:
- • Attention (e.g., Amazeen et al. 1997; Temprado et al. 1999)
- • Intention (e.g., Scholz and Kelso 1990)
- • Learning (e.g., Amazeen 2002; Zanone and Kostrubiec 2004; Newell, Liu, and Mayer-Kress 2008)
- • Handedness (e.g., Treffner and Turvey 1996)
- • Polyrhythms (e.g., Buchanan and Kelso 1993; Peper, Beek, and van Wieringen 1995; Sternad, Turvey, and Saltzman 1999)
- • Interpersonal coordination (Schmidt and Richardson 2008)
- • Cognitive modulation of coordination (Pellecchia, Shockley, and Turvey 2005; Shockley and Turvey 2005)
- • Sentence processing (e.g., Olmstead et al. 2009)
- • Speech production (Port 2003)
- • Brain–body coordination (Kelso et al. 1998)
- • Neural coordination dynamics (e.g., Jirsa, Fuchs, and Kelso 1998; Bressler and Kelso 2001; Thompson and Varela 2001; Bressler 2002)
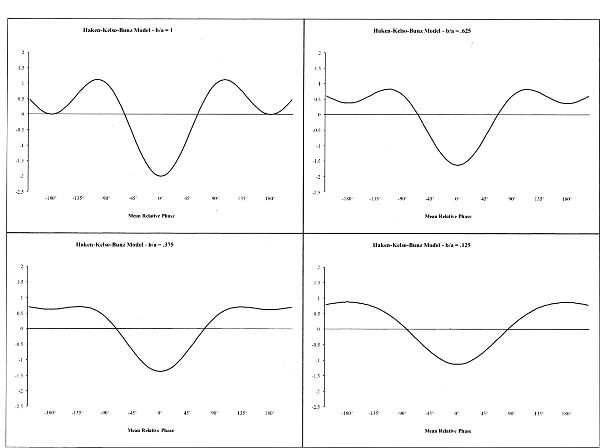
Figure 2.1. Attractor layout for the Haken-Kelso-Bunz model.
Coordination dynamics has been the most visible of the fields of application of dynamical models in the cognitive sciences, but it has hardly been the only one. Dynamical modeling has been applied to virtually every phenomenon studied in the cognitive sciences. It is well established and here to stay.
Dynamical Explanation in the Cognitive Sciences
Although not everyone would agree with me, I think that the biggest mistake I made in my 2009 book was to talk about dynamical modeling as generating explanations with no real argument that dynamical models in cognitive science could be explanations. Essentially, I underestimated the popularity of the “dynamical models are mere descriptions, not explanations” attitude toward dynamical modeling. Generally, this objection to dynamical models is made by claiming that dynamical models can only serve as covering law explanations, and rehearsing objections to covering law explanations. The reasons to object to counting dynamical models as explanations can stem from a strong theoretical commitment to computational explanation (e.g., Dietrich and Markman 2003; Adams and Aizawa 2008) or from a normative commitment to mechanistic philosophy of science (e.g., Craver 2007; Kaplan and Bechtel 2011; Kaplan and Craver 2011). Yet many cognitive scientists are committed to neither computational explanation nor normative mechanistic philosophy of science, and they can embrace dynamical explanations as genuine explanations. There is good reason to take dynamical explanations to be genuine explanations and not as mere descriptions.
Of course, dynamical explanations do not propose a causal mechanism that is shown to produce the phenomenon in question. Rather, they show that the change over time in the set of magnitudes in the world can be captured by a set of differential equations. These equations are law-like, and in some senses dynamical explanations are similar to covering law explanations (Bechtel 1998; Chemero 2000, 2009). That is, dynamical explanations show that particular phenomena could have been predicted, given local conditions and some law-like general principles.
In the case of HKB and coordination of limbs, we predict the behavior of the limbs, using the mathematical model and the settings of various parameters. Notice too that this explanation is counterfactual supporting. We can make predictions about which coordination patterns would be observed in settings that the system is not in fact in. The similarities between dynamical explanation and covering law explanation have led some commentators to argue that dynamical explanation is a kind of predictivism, according to which phenomena are explained if they could have been predicted. This claim that dynamical modeling is a kind of predictivism is followed by a two-part argument:
- 1. Rehearsals of objections to predictivism, and then
- 2. Claims that, because of these objections, dynamical models cannot be genuine explanations (Kaplan and Bechtel 2011; Kaplan and Craver 2011).
This might be an appropriate way to respond to claims that dynamical models were a genuine variety of explanations if they were written in reponse to works in which the similarities between dynamical modeling and covering law explanation were stressed (Bechtel 1998; Chemero 2000, 2009). However, the two-part argument has been made in response to discussions of dynamical models in which they were not characterized as covering law explanations (Chemero and Silberstein 2008; Stepp, Chemero, and Turvey 2011). In fact, Stepp and colleagues (2011) focus on the way that dynamical models provide explanatory unification in a sense similar to that discussed by Friedman (1974) and Kitcher (1989). (Richardson 2006 makes a similar point about biological phenomena.)
In the best dynamical explanations, an initial model of some phenomenon is reused in slightly altered form so that apparently divergent phenomena are brought under a small group of closely related models. This can be seen from the phenomena discussed earlier in “Dynamical Modeling in the Cognitive Sciences.” The cognitive phenomena accounted for by the HKB model have been previously thought to be unrelated to one another; standard cognitive phenomena such as attention and problem solving are shown to be of a piece with social interaction, motor control, language use, and neural activity. All these are accounted for with the same basic model, and as we noted earlier this model was derived from synergetics. Given this, these cognitive phenomena are also unified with other phenomena to which synergetic models have been applied—self-organizing patterns of activity in systems far from thermodynamic equilibrium. So the applications of HKB in cognitive science not only bring these apparently disparate areas of cognitive science together, they also unify these parts of cognitive science with the areas of physics, chemistry, biology, ecology, sociology, and economics that have been modeled using synergetics (see Haken 2007).
Notice, however, that the unification achieved by dynamical models such as HKB differs from that described by Friedman and Kitcher. According to both Friedman and Kitcher, unification is a way of achieving scientific reduction; as Kitcher (1989) puts it, it is a matter of reducing the number of “ultimate facts.” No such aim is served by the sort of unification one sees in dynamical modeling of the kind we have described. This is the case because the law-like generalizations of synergetics (like HKB) are scale-invariant. They are not characteristic of any particular scale and thus do not imply anything like traditional reductionism, whether ontological, intertheoretic, or in the store of ultimate facts. In the variety of unification achieved by dynamical models in cognitive science, the only thing that is reduced is the number of explanatory strategies employed. For this reason, Michael Turvey (1992) has called the strategy of consistently reapplying variants of HKB to new phenomena “strategic reductionism.” More recently, Michael Silberstein and I have described this aspect of dynamical explanation in the cognitive sciences as nonreductive unification (Silberstein and Chemero 2013).
The point of this discussion is that dynamical models do a wide array of explanatory work. They do provide descriptions, and they do allow for predictions, but they also serve the epistemic purpose of unifying a wide range of apparently dissimilar phenomena both within the cognitive sciences and between the cognitive sciences and other sciences under a small number of closely related explanatory strategies. They also serve as guides to discovery. Arguably, dynamical models do all the explanatory work that scientists are after with the exception of describing mechanisms. Only a commitment to a definitional relationship between explanation and mechanism should prevent one from accepting that the dynamical models in the cognitive sciences are genuine explanations.
This claim that dynamical explanations in cognitive science are genuine explanations is in no way intended to disparage reductionistic or mechanistic explanations. Cognitive science will need dynamical, mechanistic, and reductionistic explanations (Chemero and Silberstein 2008; Chemero 2009). To borrow a metaphor from Rick Dale, we would be puzzled if someone told us that they had an explanation of the Mississippi River (Dale 2008; Dale, Dietrich, and Chemero 2009). Because the Mississippi River is such a complex entity, we would want to know what aspect of the river they are explaining. The sedimentation patterns? The economic impact? The representation in American literature? Surely these disparate aspects of the Mississippi could not have just one explanation or even just one kind of explanation. Cognition, I submit, is just as complicated as the Mississippi River, and it would be shocking if just one style of explanation could account for all of it. For this reason, it is wise to adopt explanatory pluralism in the cognitive sciences.
Brief Interlude on Philosophical Issues in Modeling
It is worth noting here that dynamical modeling and dynamical explanation in the cognitive sciences, as just described, occupy a rather different place than modeling and simulation in other sciences. In the cognitive sciences, dynamical models are not parts of the theory, developments of the theory, or abstract experiments. Kelso, Kugler, and Turvey wanted to develop an understanding of action that was consonant with Gibson’s ecological psychology and Gibson’s claim that action is regular without being regulated. Nothing in these basic aims or in ecological psychology required modeling action as self-organization in systems far from equilibrium, which is why Kelso, Kugler, and Turvey’s decision to use these models is such an important insight. These models are not part of ecological psychology, and they were not derived from ecological psychology. Indeed, they were imported from another scientific discipline. Moreover, these models brought a host of assumptions and techniques along with them. It was these assumptions and techniques that became the engines for designing experiments and refining the models as they have been applied in the cognitive sciences.
The HKB model and later modifications of it are, as Morrison (2007) and Winsberg (2009) would say, autonomous. In fact, they are autonomous in a way that is stronger than what Morrison and Winsberg have in mind. The form of synergetics-based mathematical models that Kelso, Kugler, and Turvey import from physics are not only not developments of ecological psychological theory, they have a kind of independence from any theory, which is why they could move from physics to the cognitive sciences. This is a disagreement with Winsberg (2009), who claims that models do not go beyond the theories in which they are put to use. It is this independence that allows the models to serve as unifying explanations of phenomena, as discussed earlier in “Dynamical Explanation in the Cognitive Sciences.” This is a disagreement with Morrison (2000), who argues that explanation and unification are separate issues.
Perhaps part of the reason for these differences with Morrison and Winsberg stems from the fact that they both focus on areas of research within the physical sciences, in which theories often just take the form of nonlinear differential equations. When this is the case, one of the key roles for models is to render the equations of the theory into solvable and computationally tractable form. This is dramatically different from the role models play in the cognitive sciences, whose theories are rarely mathematical in nature. Gibson’s articulation of ecological psychology in his posthumous book (1979), which inspired Kelso, Kugler, and Turvey, had not a single equation.
It is important to note here that the claims I make in this section, indeed in this whole essay, apply only to dynamical modeling of a particular kind in a particular scientific enterprise. Models play different roles in different sciences and even in different parts of individual sciences. Philosophers of science should be modest, realizing that their claims about the relationship of models to theory and experiment might not hold in sciences other than the one from which they are drawing their current example. The relationship might not hold in a different subfield of the science they are currently discussing, and maybe not in a different research team in the same subfield. Just as it is important for cognitive scientists to acknowledge explanatory pluralism, it is important to acknowledge a kind of philosophy of science pluralism: different sciences do things differently, and lots of claims about capital-s-Science will fail to apply across the board.
Complex Systems Primer
As noted previously, the HKB model makes a series of predictions about the coordinated entities to which it is applied. One of these predictions is that there will be critical fluctuations as the coordinated system approaches a critical point—for example, just before it transitions from out-of-phase to in-phase coordination patterns. This prediction of critical fluctuation, which has been verified in nearly all the areas of human behavior and cognition listed in the dynamical modeling discussion, is perhaps the clearest way in which the use of HKB allies the cognitive sciences with the sciences of complexity. In particular, it suggests that coordinated human action arises in an interaction-dominant system (van Orden, Holden, and Turvey 2003, 2005; Riley and Holden 2012). It has also given rise to new research programs in the cognitive sciences and neurosciences concerning the character of fluctuations, a research program that promises to shed light on questions about cognition and the mind that previously seemed “merely philosophical.” In the remainder of this section I will briefly (and inadequately) set out the basic concepts and methodologies of this new research program. In the next section, I will show how, in a particular instance, those concepts and methodologies have been put into use.
First, some background: an interaction-dominant system is a highly interconnected system, each of whose components alters the dynamics of many of the others to such an extent that the effects of the interactions are more powerful than the intrinsic dynamics of the components (van Orden, Holden, and Turvey 2003). In an interaction-dominant system, inherent variability (i.e., fluctuations or noise) of any individual component C propagates through the system as a whole, altering the dynamics of the other components, say, D, E, and F. Because of the dense connections among the components of the systems, the alterations of the dynamics of D, E, and F will lead to alterations to the dynamics of component C. That initial random fluctuation of component C, in other words, will reverberate through the system for some time. So too, of course, would nonrandom changes in the dynamics of component C. This tendency for reverberations gives interaction-dominant systems what is referred to as “long memory” (Chen, Ding, and Kelso 1997).
In contrast, a system without this dense dynamical feedback, a component-dominant system, would not show this long memory. For example, imagine a computer program that controls a robotic arm. Although noise that creeps into the commands sent from the computer to the arm might lead to a weld that misses its intended mark by a few millimeters, that missed weld will not alter the behavior of the program when it is time for the next weld. Component-dominant systems do not have long memory. Moreover, in interaction-dominant systems one cannot treat the components of the system in isolation: because of the widespread feedback in interaction-dominant systems, one cannot isolate components to determine exactly what their contribution is to particular behavior. And because the effects of interactions are more powerful than the intrinsic dynamics of the components, the behavior of the components in any particular interaction-dominant system is not predictable from their behavior in isolation or from their behavior in some other interaction-dominant system. Interaction-dominant systems, in other words, are not modular. Indeed, they are in a deep way unified in that the responsibility for system behavior is distributed across all the components. As will be discussed later, this unity of interaction-dominant systems has been used to make strong claims about the nature of human cognition (van Orden, Holden, and Turvey 2003, 2005; Holden, van Orden, and Turvey 2009; Riley and Holden 2012).
In order to use the unity of interaction-dominant systems to make strong claims about cognition, it has to be argued that cognitive systems are, at least sometimes, interaction dominant. This is where the critical fluctuations posited by the HKB model come in. Interaction-dominant systems self-organize, and some will exhibit self-organized criticality. Self-organized criticality is the tendency of an interaction-dominant system to maintain itself near critical boundaries so that small changes in the system or its environment can lead to large changes in overall system behavior. It is easy to see why self-organized criticality would be a useful feature for behavioral control: a system near a critical boundary has built-in behavioral flexibility because it can easily cross the boundary to switch behaviors (e.g., going from out-of-phase to in-phase coordination patterns). (See Holden, van Orden, and Turvey 2009 and Kello, Anderson, Holden, and van Orden 2008 for further discussion.)
It has long been known that self-organized critical systems exhibit a special variety of fluctuation called 1/f noise or pink noise (Bak, Tang, and Wieseneld 1988). That is, 1/f noise or pink noise is a kind of not-quite-random, correlated noise, halfway between genuine randomness (white noise) and a drunkard’s walk, in which each behavior is constrained by the prior one (brown noise). Often 1/f noise is described as a fractal structure in a time series, in which the variability at a short time scale is correlated with variability at a longer time scale. In fact, interaction-dominant dynamics predicts that this 1/f noise would be present. As discussed previously, the fluctuations in an interaction-dominant system percolate through the system over time, leading to the kind of correlated structure to variability that is 1/f noise. Here, then, is the way to infer that cognitive and neural systems are interaction dominant: exhibiting 1/f noise is evidence that a system is interaction dominant.
This suggests that the mounting evidence that 1/f noise is ubiquitous in human physiological systems, behavior, and neural activity is also evidence that human physiological, cognitive, and neural systems are interaction dominant. To be clear, there are ways other than interaction-dominant dynamics to generate 1/f noise. Simulations show that carefully gerrymandered component-dominant systems can exhibit 1/f noise (Wagenmakers, Farrell, and Ratcliff 2005). But such gerrymandered systems are not developed from any physiological, cognitive, or neurological principle and so are not taken to be plausible mechanisms for the widespread 1/f noise in human physiology, brains, and behavior (van Orden, Holden, and Turvey 2005). So the inference from 1/f noise to interaction dominance is not foolproof, but there currently is no plausible explanation of the prevalence of 1/f noise other than interaction dominance. Better than an inference to the best explanation, that 1/f noise indicates interaction-dominant dynamics is an inference to the only explanation.
Heidegger in the Laboratory
Dobromir Dotov, Lin Nie, and I have recently used the relationship between 1/f noise and interaction dominance to empirically test a claim that can be derived from Heidegger’s phenomenological philosophy (1927/1962; see Dotov, Nie, and Chemero 2010; Nie, Dotov, and Chemero 2011). In particular, we wanted to see whether we could gather evidence supporting the transition Heidegger proposed for “ready-to-hand” and “unready-to-hand” interactions with tools. Heidegger argued that most of our experience of tools is unreflective, smooth coping with them. When we ride a bicycle competently, for example, we are not aware of the bicycle but of the street, the traffic conditions, and our route home. The bicycle itself recedes in our experience and becomes the thing through which we experience the road. In Heidegger’s language, the bicycle is ready-to-hand, and we experience it as a part of us, no different than our feet pushing the pedals. Sometimes, however, the derailleur does not respond right away to an attempt to shift gears or the brakes grab more forcefully than usual, so the bicycle becomes temporarily prominent in our experience—we notice the bicycle. Heidegger would say that the bicycle has become unready-to-hand, in that our smooth use of it has been interrupted temporarily and it has become, for a short time, the object of our experience. (In a more permanent breakdown in which the bicycle becomes unuseable, like a flat tire, we experience it as present-at-hand.)
To gather empirical evidence for this transition, we relied on dynamical modeling that uses the presence of 1/f noise or pink noise as a signal of sound physiological functioning (e.g., West 2006). As noted previously, 1/f noise or pink noise is a kind of not-quite-random, correlated noise, halfway between genuine randomness (white noise) and a drunkard’s walk, in which each fluctuation is constrained by the prior one (brown noise). Often 1/f noise is described as a fractal structure in a time series in which the variability at a short time scale is correlated with variability at a longer time scale. (See Riley and Holden 2012 for an overview.) The connection between sound physiological functioning and 1/f noise allows for a prediction related to Heidegger’s transition: when interactions with a tool are ready-to-hand, the human-plus-tool should form a single interaction-dominant system; this human-plus-tool system should exhibit 1/f noise.
We showed this to be the case by having participants play a simple video game in which they used a mouse to control a cursor on a monitor. Their task was to move the cursor so as to “herd” moving objects to a circle on the center of the monitor. At some point during the trial, the connection between the mouse and cursor was temporarily disrupted so that movements of the cursor did not correspond to movements of the mouse, before returning to normal. The primary variable of interest in the experiment was the accelerations of the hand-on-the-mouse. Accelerations are of special interest because they correspond to purposeful actions on the part of the participant, when she changes the way her hand is moving. Instantaneous accelerations in three dimensions were measured at 875 Hz. We used only horizontal accelerations (i.e., left to right), using a 60 Hz low-pass filter to eliminate variability that was not from behavior, and then we down-sampled the data by a factor of 10. This gave us a time series of accelerations. This time series was subjected to detrended fluctuation analysis (DFA). In DFA, the time series is divided into temporal intervals of sizes varying from one second to the size of the whole time series. For each interval size, the time series is divided into intervals of that size, and within each of those intervals a trend line is calculated. The fluctuation function F(n) for each interval size n is the root mean square of the variability from the trend line within each interval of that size. F(n) is calculated for intervals of 1, 2, 4, 8, 16 . . . seconds. As you would expect, F(n) increases as the interval size increases.
The values of F(n) were plotted against the interval size in a log-log plot (Figure 2.2). The slope of the trend line in that log-log plot is the primary output of DFA, called a Hurst exponent. Hurst exponents of approximately 1 indicate the presence of 1/f noise, with lower values indicating white noise and higher values indicating brown noise. The raw data are folded, spindled, and mutilated to determine whether the system exhibits 1/f noise and can be assumed to be interaction dominant.
As predicted, the hand–mouse movements of the participants exhibited 1/f noise while the video game was working correctly. The 1/f noise decreased, almost to the point of exhibiting pure white noise, during the mouse perturbation. So while the participants were smoothly playing the video game, they were part of a human–computer interaction-dominant system; when we temporarily disrupted performance, that pattern of variability temporarily disappeared. This is evidence that the mouse was experienced as ready-to-hand while it was working correctly and became unready-to-hand during the perturbation. (See Dotov, Nie, and Chemero 2010; Nie, Dotov, and Chemero 2011; and Dotov et al. 2017.)
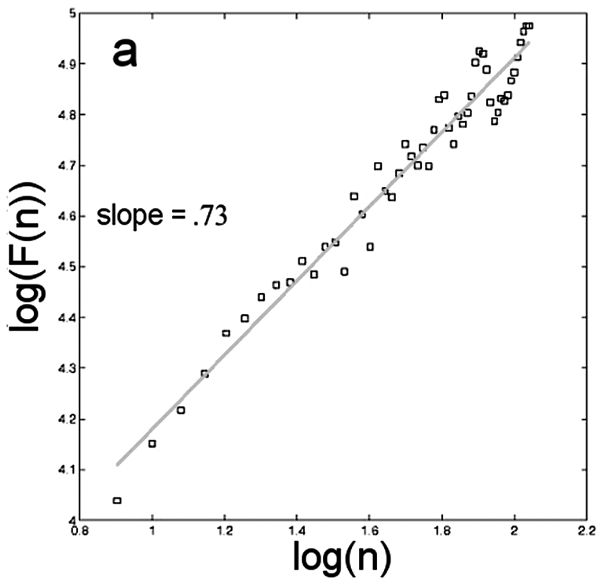
Figure 2.2. Detrended fluctuation analysis (DFA) plot for a representative participant in Dotov, Nie, and Chemero (2010).
It is important to note the role of the dynamical modeling. The dynamical model was used to put Heidegger’s claims about phenomenology into touch with potentially gatherable data. In this case, after several unsuccessful attempts to demonstrate Heidegger’s ideas and the thesis of extended cognition, we learned about the use of detrended fluctuation analysis and 1/f noise. Understanding the claims that could be made using detrended fluctuation analysis led us to design our experimental task in the way that we did. In effect, the models made Heidegger’s claims empirically accessible and allowed us to gather evidence for them. Moreover, the results from prior dynamical modeling acted as a guide to discovery, a source of new hypotheses for further experimental testing (Chemero 2000, 2009). In this case, the findings concerning 1/f noise and physiology and the knowledge of the way 1/f noise could be detected inspired the experimental task. This makes clear that the dynamical models are not acting as mere descriptions of data nor even only as tools for analyzing data after they have been gathered; rather, dynamical models play a significant role in hypothesis generation. This is the point that is apparent especially to those who are both modelers and philosophers of science, such as Isabelle Peschard (2007).
Data and Noise, and Noise
For current purposes, the findings about Heidegger’s phenomenology and role of mathematical modeling in hypothesis generation are of secondary importance. What matters more is what happened to the data along the way. As noted earlier, the data we gathered concerned the accelerations of a hand on a computer mouse. Though these movements were gathered in three dimensions, only one (side-to-side) dimension was used. Of the other two dimensions, only one was significant: the mouse moved along the surface of a table, so up-down accelerations would be negligible. But one would think that the third dimension (front-back) would be very important.
All the participants were moving their hands in every direction along the surface of the table, and only very rarely were they moving them purely side-to-side or front-back. So the acceleration data, as we collected it, does not capture the actual behavior of the participants. We could, of course, have recovered the actual two-dimensional instantaneous accelerations computationally, but we did not. The reason we did not was because we did not care about how the participants moved their hands while they played the video game; we also did not care how well they played the video game. What we cared about were the fluctuations in their hand movements rather than the actual hand movements. That is, we cared about the noise, not the data.
Indeed, getting rid of the data and leaving only the noise is the purpose of detrended fluctuation analysis. It is a step-by-step procedure to eliminate anything about the time series other than the noise, and then to determine the character of that noise, whether it is white, pink, or brown. Consider again the detrending part of DFA: within each time interval, the linear trend is determined, and that trend line is subtracted from each instantaneous acceleration. If we cared about the actual hand movements, the trend line itself would be the object of interest because it would let us know how a participant moved her hand on the mouse during any particular time interval. But the actual movements of the hand on the mouse are not relevant to answering the questions we wanted to answer, that the methods of complex systems science allowed us to answer. That is, by ignoring the data and focusing on the noise we were able to argue that the participant–computer system formed a single interaction-dominant system, and to provide some empirical confirmation of a portion of Heidegger’s phenomenology.
Given the rate at which methods from complex systems methods are being brought into cognitive sciences, we have good reason to doubt the general truth of the methodological truism that psychology students are commonly taught—that is, that a good experiment maximizes primary variance and minimizes noise. This is certainly an issue that psychologists and psychology teachers ought to be concerned with. Of course, at an introductory level, many complexities are papered over, often so much so that what we tell students is not strictly speaking true. Unfortunately, many practicing scientists take what I call the methodological truism to be a truth. It is not. Really, the widespread use of complex systems methods should introduce large changes to the way experiments are designed in the cognitive sciences. This is the case because analyses such as DFA involve a violation of the assumptions of the generalized linear model that undergirds the statistics used to analyze their outputs (such as analysis of variance, multivariate analysis of variance, regressions, etc.). In particular, because DFA is applied to systems with “long memory” (i.e., systems in which the outcome of any particular observation is connected to the outcome of other observations) the observations are not independent of one another as is required by the generalized linear model. As just noted, this is an issue well outside the scope of what an introductory-level student needs to know, but it is an issue nonetheless.
What is more of an issue for philosophers of science is that we have good reason to call the distinction between data and noise into question. This is problematic because that distinction is so deeply built into the practice of cognitive scientists—and indeed all scientists. There are error bars on most graphs and noise terms in most mathematical models. In every data set, that is, the assumption is that there is something like what Bogen and Woodward (1988) call the phenomenon—which the scientist cares about—and the noise—which she does not care about. When complex systems methods are used in the cognitive sciences, as we have seen, noise is the phenomenon.
Bogen (2010) makes a similar point that sometimes the noise is what scientists care about. This much is clear from Figure 2.2. Recall that DFA produces a log-log plot of fluctuations against interval sizes. The slope of a trend line on that plot is the Hurst exponent, the value of which lets you know whether 1/f noise is present. Very few of the points shown in Figure 2.2 are actually on that trend line, and we could easily calculate the goodness of fit of that trend line. That is, after we have removed all the data about the actual hand movements using DFA and made the character of the noise in hand movements the object of our interest, there is still further noise. So when the phenomenon the scientist cares about is noise, there is second-order noise that she does not care about.
It seems that one could re-establish the distinction between data and noise, but only in terms of the explanatory interests of scientists. Data are the outcomes of observations, measurements, and manipulations that the scientist cares about. Sometimes these outcomes will be measures of fluctuations, what has traditionally been called noise. Noise, then, will be variability in the outcomes of those measurements and manipulations that the scientist does not care about. If a scientist (or someone like me who occasionally pretends to be a scientist) cares about confirming some claims derived from Heidegger’s phenomenology by showing that humans and computers together can comprise unified, interaction-dominant systems, he will take Hurst exponents to be data, even though they are measurements of noise. He will then take error in the linear regression used to produce the Hurst exponent as noise. Understanding noise this way—as ignored variability in what the scientist cares about—makes distinguishing data from noise of a piece with the problem of relevance that Peschard discusses (2010, 2012). Whether something is data or noise depends on what scientists are interested in, and what they think matters to the phenomena they are exploring.
The Methodological Truism, Again
The cognitive sciences are young sciences, with a creation mythology that places their beginning in 1956. Psychology is a bit older, having begun in earnest in the late nineteenth century. Yet it seems that cognitive scientists and psychologists have already gathered the majority of the low-hanging fruit, and the interesting findings that can be had with timing experiments and t-tests have mostly been found. It is for this reason that new experimental and analytical techniques are being brought into the cognitive sciences from the sciences of complexity.
In this essay, I have looked at some consequences of the import into the cognitive sciences of tools from synergetics. There are, I have suggested, consequences both for the cognitive sciences and for the philosophy thereof. I want to close by reconsidering what I called the “methodological truism” in the first section. I repeat it here.
The goal of a good experiment is to maximize primary variance, eliminate secondary variance, and minimize error variance.
What I hope to have shown in this essay is that teaching students in introductory psychology the methodological truism is a lot like telling young children that babies are delivered by storks. It is something that was thought to be good enough until the hearers were mature enough to know the messy, complicated truth about things. Unfortunately, the story is not just untrue, but it covers up all the interesting stuff. And, of course, we adults should know better.
References
Adams, Fredrick, and Kenneth Aizawa. 2008. The Bounds of Cognition. Malden, Mass.: Blackwell.
Amazeen, Eric L., Polemnia G. Amazeen, Paul J. Treffner, and Michael T. Turvey. 1997. “Attention and Handedness in Bimanual Coordination Dynamics.” Journal of Experimental Psychology: Human Perception and Performance 23: 1552–60.
Amazeen, Polemnia G. 2002. “Is Dynamics the Content of a Generalized Motor Program for Rhythmic Interlimb Coordination?” Journal of Motor Behavior 34: 233–51.
Bak, Per, Chao Tang, and Kurt Wiesenfeld. 1988. “Self-Organized Criticality.” Physical Review A 38: 364–74.
Bechtel, William. 1998. “Representations and Cognitive Explanations: Assessing the Dynamicist Challenge in Cognitive Science.” Cognitive Science 22: 295–318.
Bogen, James. 2010. “Noise in the World.” Philosophy of Science 77: 778–91.
Bogen, James, and James Woodward. 1988. “Saving the Phenomena.” Philosophical Review 97: 303–52.
Bressler, Steven L. 2002. “Understanding Cognition through Large-Scale Cortical Networks.” Current Directions in Psychological Science 11: 58–61.
Bressler, Steven L., and J. A. Scott Kelso. 2001. “Cortical Coordination Dynamics and Cognition.” Trends in Cognitive Sciences 5: 26–36.
Buchanan, J. J., and J. A. Scott Kelso. 1993. “Posturally Induced Transitions in Rhythmic Multijoint Limb Movements.” Experimental Brain Research 94: 131–42.
Chemero, Anthony. 2000. “Anti-representationalism and the Dynamical Stance.” Philosophy of Science 67: 625–47.
Chemero, Anthony. 2009. Radical Embodied Cognitive Science. Cambridge, Mass.: MIT Press.
Chemero, Anthony, and Michael Silberstein. 2008. “After the Philosophy of Mind: Replacing Scholasticism with Science.” Philosophy of Science 75: 1–27.
Chen, Yanqing, Mingzhou Ding, and J. A. Scott Kelso. 1997. “Long Memory Processes 1/fα Type in Human Coordination.” Physical Review Letters 79: 4501–4.
Craver, Carl. 2007. Explaining the Brain: What a Science of the Mind-Brain Could Be. New York: Oxford University Press.
Dale, Rick. 2008. “The Possibility of a Pluralist Cognitive Science.” Journal of Experimental and Theoretical Artificial Intelligence 20: 155–79.
Dale, Rick, Eric Dietrich, and Anthony Chemero. 2009. “Pluralism in the Cognitive Sciences.” Cognitive Science 33: 739–42.
Dietrich, Eric, and Arthur B. Markman. 2003. “Discrete Thoughts: Why Cognition Must Use Discrete Representations.” Mind and Language 18: 95–119.
Dotov, Dobromir G., Lin Nie, and Anthony Chemero. 2010. “A Demonstration of the Transition from Ready-to-Hand to Unready-to-Hand.” PLoS ONE 5: e9433.
Dotov, Dobromir G., Lin Nie, Kevin Wojcik, Anastasia Jinks, Xiaoyu Yu, and Anthony Chemero. 2017. “Cognitive and Movement Measures Reflect the Transition to Presence-at-Hand.” New Ideas in Psychology 45: 1–10.
Franklin and Marshall College Psychology Department. Introduction to Psychology Laboratory Manual. Unpublished.
Friedman, Michael. 1974. “Explanation and Scientific Understanding.” Journal of Philosophy 71: 5–19.
Gibson, James J. 1979. The Ecological Approach to Visual Perception. Boston: Houghton-Mifflin.
Haken, Hermann. 2007. “Synergetics.” Scholarpedia 2: 1400.
Haken, Hermann, J. A. Scott Kelso, and H. Bunz. 1985. “A Theoretical Model of Phase Transitions in Human Hand Movements.” Biological Cybernetics 51: 347–56.
Heidegger, Martin. (1927) 1962. Being and Time. Translated by J. Macquarrie and E. Robinson. New York: Harper & Row. First published in 1927 as Sein und Zeit.
Holden, John G., Guy C. Van Orden, and Michael T. Turvey. 2009. “Dispersion of Response Times Reveals Cognitive Dynamics.” Psychological Review 116: 318–42.
Iverson, Jana M., and Esther Thelen. 1999. “Hand, Mouth, and Brain: The Dynamic Emergence of Speech and Gesture.” Journal of Consciousness Studies 6: 19–40.
Jirsa, Viktor K., Armin Fuchs, and J. A. Scott Kelso. 1998. “Connecting Cortical and Behavioral Dynamics: Bimanual Coordination.” Neural Computation 10: 2019–45.
Kaplan, David M., and William Bechtel. 2011. “Dynamical Models: An Alternative or Complement to Mechanistic Explanations?” Topics in Cognitive Science 3: 438–44.
Kaplan, David M., and Carl Craver. 2011. “The Explanatory Force of Dynamical and Mathematical Models in Neuroscience: A Mechanistic Perspective.” Philosophy of Science 78: 601–28.
Kello, Christopher T., Gregory G. Anderson, John G. Holden, and Guy C. van Orden. 2008. “The Pervasiveness of 1/f Scaling in Speech Reflects the Metastable Basis of Cognition.” Cognitive Science 32: 1217–31.
Kelso, J. A. Scott. 1984. “Phase Transitions and Critical Behavior in Human Bimanual Coordination.” American Journal of Physiology—Regulatory, Integrative and Comparative Physiology 246: R1000–4.
Kelso, J. A. Scott. 1995. Dynamic Patterns: The Self-Organization of Brain and Behavior. Cambridge, Mass.: MIT Press.
Kelso, J. A. Scott, A. Fuchs, T. Holroyd, R. Lancaster, D. Cheyne, and H. Weinberg. 1998. “Dynamic Cortical Activity in the Human Brain Reveals Motor Equivalence.” Nature 23: 814–18.
Kitcher, Philip. 1989. “Explanatory Unification and the Causal Structure of the World.” In Scientific Explanation, edited by Philip Kitcher and Wesley C. Salmon, 410–505. Minneapolis: University of Minnesota Press.
Kugler, Peter N., and Michael T. Turvey. 1987. Information, Natural Law, and the Self-Assembly of Rhythmic Movement. Hillsdale, N.J.: Erlbaum.
Kugler, Peter N., J. A. Scott Kelso, and Michael T. Turvey. 1980. “On the Concept of Coordinative Structures as Dissipative Structures. I. Theoretical Lines of Convergence.” In Tutorials in Motor Behavior, edited by G. E. Stelmach and J. Requin, 3–47. Amsterdam: North Holland.
Morrison, Margaret. 2000. Unifying Scientific Theories. Cambridge: Cambridge University Press.
Morrison, Margaret. 2007. “Where Have All the Theories Gone?” Philosophy of Science 74: 195–228.
Newell, Karl M., Yeou-Teh Liu, and Gottfried Mayer-Kress. 2008. “Landscapes beyond the HKB Model.” In Coordination: Neural, Behavioral and Social Dynamics, edited by Armin Fuchs and Viktor K. Jirsa, 27–44. Heidelberg: Springer-Verlag.
Nie, Lin, Dobromir G. Dotov, and Anthony Chemero. 2011. “Readiness-to-Hand, Extended Cognition, and Multifractality.” In Proceedings of the 33rd Annual Meeting of the Cognitive Science Society, edited by Laura Carlson, Christoph Hölscher, and Thomas F. Shipley, 1835–40. Austin, Tex.: Cognitive Science Society.
Olmstead, Anne J., Navin Viswanathan, Karen A. Aicher, and Carol A. Fowler. 2009. “Sentence Comprehension Affects the Dynamics of Bimanual Coordination: Implications for Embodied Cognition.” Quarterly Journal of Experimental Psychology 62: 2409–17.
Pellecchia, Geraldine L., Kevin Shockley, and Michael T. Turvey. 2005. “Concurrent Cognitive Task Modulates Coordination Dynamics.” Cognitive Science 29: 531–57.
Peper, C. Lieke E., Peter J. Beek, and Piet C. W. van Wieringen. 1995. “Coupling Strength in Tapping a 2:3 Polyrhythm.” Human Movement Science 14: 217–45.
Peschard, Isabelle. 2007. “The Values of a Story: Theories, Models, and Cognitive Values.” Principia 11: 151–69.
Peschard, Isabelle. 2010. “Target Systems, Phenomena and the Problem of Relevance.” Modern Schoolman 87: 267–84.
Peschard, Isabelle. 2012. “Forging Model/World Relations: Relevance and Reliability.” Philosophy of Science 79: 749–60.
Port, Robert F. 2003. “Meter and Speech.” Journal of Phonetics 31: 599–611.
Port, Robert F., and Timothy van Gelder. 1996. Mind as Motion. Cambridge, Mass.: MIT Press.
Richardson, Robert C. 2006. “Explanation and Causality in Self-Organizing Systems.” In Self-Organization and Emergence in Life Sciences, edited by Bernard Feltz, Marc Crommelinck, and Philippe Goujon, 315–40. Dordrecht, the Netherlands: Springer.
Riley, Michael A., and John G. Holden. 2012. “Dynamics of Cognition.” WIREs Cognitive Science 3: 593–606.
Schmidt, Richard C., and Michael J. Richardson. 2008. “Dynamics of Interpersonal Coordination.” In Coordination: Neural, Behavioral and Social Dynamics, edited by Armin Fuchs and Viktor K. Jirsa, 281–308. Heidelberg: Springer-Verlag.
Scholz, J. P., and J. A. Scott Kelso. 1990. “Intentional Switching between Patterns of Bimanual Coordination Depends on the Intrinsic Dynamics of the Patterns.” Journal of Motor Behavior 22: 98–124.
Shockley, Kevin, and Michael T. Turvey. 2005. “Encoding and Retrieval during Bimanual Rhythmic Coordination.” Journal of Experimental Psychology: Learning, Memory, and Cognition 31: 980–90.
Silberstein, Michael, and Anthony Chemero. 2013. “Constraints on Localization and Decomposition as Explanatory Strategies in the Biological Sciences.” Philosophy of Science 80: 958–70.
Stepp, Nigel, Anthony Chemero, and Michael T. Turvey. 2011. “Philosophy for the Rest of Cognitive Science.” Topics in Cognitive Science 3: 425–37.
Sternad, Dagmar, Michael T. Turvey, and Elliot L. Saltzman. 1999. “Dynamics of 1:2 Coordination: Generalizing Relative Phase to n:m Rhythms.” Journal of Motor Behavior 31: 207–24.
Temprado, Jean-Jacques, Pier-Giorgio Zanone, Audrey Monno, and Michel Laurent. 1999. “Attentional Load Associated with Performing and Stabilizing Preferred Bimanual Patterns.” Journal of Experimental Psychology: Human Perception and Performance 25: 1579–94.
Thompson, Evan, and Francisco J. Varela. 2001. “Radical Embodiment: Neural Dynamics and Consciousness.” Trends in Cognitive Sciences 5: 418–25.
Treffner, P. J., and M. T. Turvey. 1996. “Symmetry, Broken Symmetry, and Handedness in Bimanual Coordination Dynamics.” Experimental Brain Research 107: 163–78.
Turvey, Michael T. 1992. “Affordances and Prospective Control: An Outline of the Ontology.” Ecological Psychology 4: 173–87.
van Gelder, Timothy. 1995. “What Might Cognition Be if Not Computation?” Journal of Philosophy 91: 345–81.
van Gelder, Timothy. 1998. “The Dynamical Hypothesis in Cognitive Science.” Behavioral and Brain Sciences 21: 615–28.
Van Orden, Guy C., John G. Holden, and Michael T. Turvey. 2003. “Self-Organization of Cognitive Performance.” Journal of Experimental Psychology: General 132: 331–51.
Van Orden, Guy C., John G. Holden, and Michael T. Turvey. 2005. “Human Cognition and 1/f Scaling.” Journal of Experimental Psychology: General 134: 117–23.
Von Holst, Erich. (1935) 1973. The Behavioral Physiology of Animal and Man: The Collected Papers of Erich Von Holst, vol. 1. Coral Gables, Fla.: University of Miami Press.
Wagenmakers, Eric-Jan, Simon Farrell, and Roger Ratcliff. 2005. “Human Cognition and a Pile of Sand: A Discussion on Serial Correlations and Self-Organized Criticality.” Journal of Experimental Psychology: General 134: 108–16.
West, Bruce J. 2006. “Fractal Physiology, Complexity, and the Fractional Calculus.” In Fractals, Diffusion and Relaxation in Disordered Complex Systems, edited by Y. Kalmykov, W. Coffey, and S. Rice, 1–92. Singapore: Wiley-Interscience.
Winsberg, Eric. 2009. Science in the Age of Computer Simulation. Chicago: University of Chicago Press.
Zanone, Pier-Giorgio, and Viviane Kostrubiec. 2004. “Searching for (Dynamic) Principles of Learning.” In Coordination Dynamics: Issues and Trends, edited by Viktor K. Jiras and J. A. Scott Kelso, 57–89. Heidelberg: Springer Verlag.