1
Models of Experiments
Ronald N. Giere
In the logical empiricist philosophy of science, the primary epistemological relationship was between a theory, T, and an observation, O. Both were understood as some sort of linguistic entities—sentences, statements, propositions, whatever. With the increasing emphasis on models within the philosophy of science, this relationship has increasingly been replaced by one between theoretical models and models of data. Moreover, following Suppes’s (1962) long ago advice, it has been emphasized that there is a hierarchy of theoretical models, ranging from very general to very specific, between high level theoretical models and models of data. During roughly the same period as models came to the fore within the philosophy of science, some philosophers of science, together with sociologists and historians of science, independently developed an interest in experimentation. Only belatedly has it been realized that perhaps in some place in the hierarchy of models there should be a model of the experiment. This discussion explores that possibility.
In fact, the expression “model of the experiment” appears already in Suppes’s 1962 article. It turns out to be something fairly abstract. Imagine an experiment (Suppes’s example was taken from behaviorist learning theory) with a binary experimental variable and just two possible results on a particular trial. There are then four possible states for each trial, thus 4n possible different series of n trials. Very roughly, Suppes identifies “the theory of the experiment” with this set of possible series. A model of the experiment is then a particular series that might be the realization of an actual experiment. What I have in mind is something far less abstract.
Closer to the mark is what Allan Franklin called a “theory of the apparatus” in his early work on the philosophy of experimentation (1986, 168). His idea was that a “well-confirmed theory of the apparatus” may give us reason to believe the results of experiments using that apparatus. I expect many others have subsequently invoked a similar idea. It is surely implicit in Ian Hacking’s founding philosophical work on experimentation (1983). But concentrating on an apparatus seems still too narrow a focus for an account of a model of an experiment. If we are to incorporate experimentation into a model-based philosophy of science, we will need something broader.
A Hierarchy of Models
Figure 1.1 is my attempt to create a Suppes-like hierarchy of models incorporating a model of the experiment. It is clear that, in any particular case, the model of the experiment must be at the bottom of the hierarchy. The nature of the experiment determines what one might call the “form” of the data. That is, the experiment determines what kind of data will be acquired and, in the case of numerical data, the range of possible values of any particular data point. But before saying more about models of experiments, a word about the rest of the hierarchy is required.
As I understand this hierarchy, the principled models at the top are defined by what are usually called the “laws” of the science in question, such as Newton’s laws or Maxwell’s equations. The laws define a type of system instantiated abstractly in the principled models (a “theoretical perspective”). Adding further conditions, such as force functions in the case of classical mechanics, yields representational models. Representational models apply to designated real systems, or types of systems, with the features of these systems interpreted and identified in terms that define the principled models. Eventually this hierarchy reaches a fully specified representational model of a particular system involved in an experiment. It is this model that is compared with a model of the data generated by an experiment in order to decide how well the representational model fits the real system under investigation.
This picture presumes a unified mature science that includes high-level principles that can be fitted out for different circumstances. It is possible to construct hierarchies for cases in which multiple principles from different sciences are involved, or in which there are no general principles at all and thus no principled models.[1]
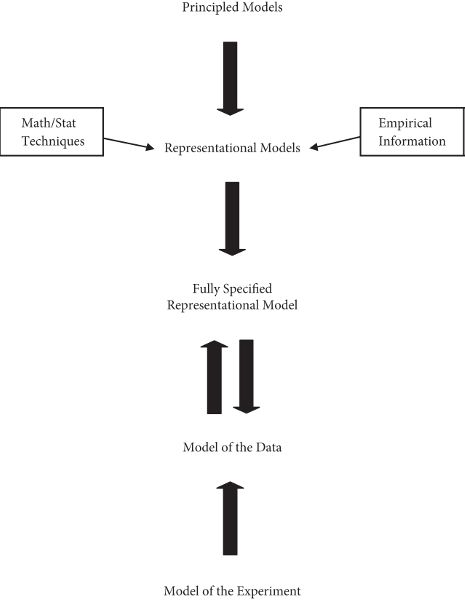
Figure 1.1. A Suppes-like hierarchy of models incorporating a model of the experiment.
In recognition of the messiness of applying abstract theoretical models (e.g., Morgan and Morrison 1999), I have included reference to the various mathematical and statistical techniques involved in making the many approximations and idealizations typically involved in eventually reaching a model of a specific real system. Also included is reference to the fact that aspects of models from other disciplines as well as empirical generalizations may need to be incorporated in the process. The details of this process are represented by the light horizontal arrows. The top two thick arrows pointing downward include deduction, but much else besides. The thick arrow going up from the model of the experiment represents the constraints the experiment places on any possible model of the data. Finally, up and down arrows between the model of the data and the fully specified representational model represent a comparison, and perhaps mutual adjustment, of these two models.
I think it would be a mistake to “flatten” the representation of experimenting with models to the extent that one loses any sense of an underlying hierarchical structure. Keeping the hierarchy turns out to be very useful in locating a model of the experiment in our understanding of experimenting with models.

Figure 1.1 realizes Suppes’s idea of science as involving a hierarchy of models. Necessarily missing from the figure, however, is any representation of interaction with the world. Thus, although there is a model of the data, the data are not represented in the hierarchy. Models are entities, typically abstract, humanly constructed for many purposes, but prominently for representing aspects of the world. The data are one such aspect. To fill out the picture, I think we need a parallel, but separate, hierarchy, a physical rather than symbolic hierarchy. Figure 1.2 shows one possibility. It is the recorded data, of course, that are used to construct the model of the data in the Suppes hierarchy. Here the vertical arrows represent physical processes, but, of course, the data have to be “interpreted” in terms of the model of the data.
Models of Experiments
To proceed further it will help to introduce an example. Here I will invoke a contemporary experiment that I have explored in some detail elsewhere, observations with instruments aboard the satellite based Compton Gamma Ray Observatory.[2] The general theory that motivates this particular experiment is that heavy elements are produced inside very large stars. One such is a radioactive isotope of aluminum that decays with a distinctive emission of a 1.8 MeV Gamma Ray. The nearest example of large star formation is the center of our Milky Way galaxy. Thus, the observation of 1.8 MeV Gamma Rays from this source would provide direct confirmation of the theory of heavy element formation in stars. Figure 1.3 shows a Suppes hierarchy for this example.
Now we can begin to consider what a model of this experiment might be like. Here I will distinguish three categories of components that I think must be represented in any model of an experiment of this scope: material, computational, and agential (done by human agents).
Material Components
Material components include what in more traditional experiments are called “the apparatus.” The primary material component in this case is the Compton Observatory itself, which includes four different detectors. I will focus on just one, the Compton Gamma Ray Telescope, or COMPTEL. As its name indicates, this instrument detects gamma rays by means of the Compton effect, the interaction of a gamma ray with an electron, which, moving through an appropriate substance, gives off light whose intensity can be measured and used to compute the energy of the incoming gamma ray. Using two levels of detectors, one can determine the angle at which the gamma ray entered the instrument, thus locating its source in the heavens. This requires complex coincidence–anticoincidence circuitry to ensure that it is the same gamma ray being detected twice, the second time with diminished energy.
The point here is that the knowledge required to develop a model of the instrument (just part of “the experiment”) is different from that to which the experiment is meant to contribute—in this case, models of higher element formation in stars. So although I have located the model of the experiment at the bottom of a Suppes hierarchy (see Figure 1.1), the construction of this model takes one far outside the initial hierarchy. In fact, we can construct a completely different hierarchy of models leading to a model of the instrument, as shown in Figure 1.4.
In this case, the references to mathematical techniques and empirical information are mere markers for a world of engineering models and techniques beyond the ken of most philosophers of science.[3] The downward arrows represent a correspondingly complex process leading finally to a model of COMPTEL. Note, finally, that this hierarchy is just one component of a comprehensive model of the experiment.
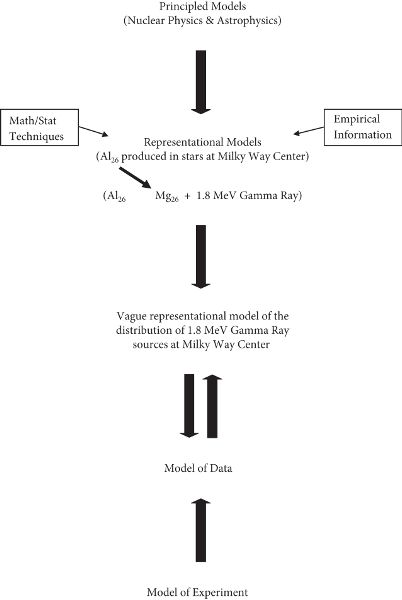
Figure 1.3. Suppes hierarchy for heavy element formation in stars.
Computational Components
The whole experiment incorporates a vast computational network extending from the initial data acquisition to the final output as a computer graphic. Moreover, this network is vastly extended in both space and time. The telescope itself is, of course, in Earth orbit. Then there are relay satellites transmitting data down to earth stations in, for example, White Sands, New Mexico. Finally the data are analyzed at the Space Telescope Science Institute in Greenbelt, Maryland. On a temporal scale, some experiments include data acquired over months, even years. A model of this network, at least in schematic form, must be part of the final model of the experiment. And here again, one is appealing to knowledge completely outside the original Suppes hierarchy.
Agential Components
It obviously takes a great number of people to run a modern experiment as well as complex organization and careful planning. Perhaps the most salient role for agents is in the interpretation of the results, the comparison of the data model with relevant theoretical models. My own preference is to regard this not as any sort of logical inference but as individual and collective decision making—deciding what to conclude about the relative fit of theoretical models with the world, and with what degree of confidence.[4]
Overall, I would regard the operation of an experiment as a case of distributed cognition and the whole experimental setup as a distributed cognitive system.[5] The important point here, however, is that, once again, constructing a model of the experiment requires drawing on concepts and knowledge well beyond the original Suppes hierarchy.
Understanding the Data Model
It has always been true that understanding the data from any experiment requires knowledge of the process that produced it. The framework of connecting a data model with a model of the experiment gives prominence to this fact and provides a vocabulary for thinking about it. In the case of COMPTEL, perhaps the most important scientific fact about the process is that it is based on Compton scattering. The rest is engineering, but of course it is the engineering that produces the accuracy in measurements of the energy of gamma rays and the location of the sources. The primary lesson is that understanding a data model requires understanding a model of the experiment.
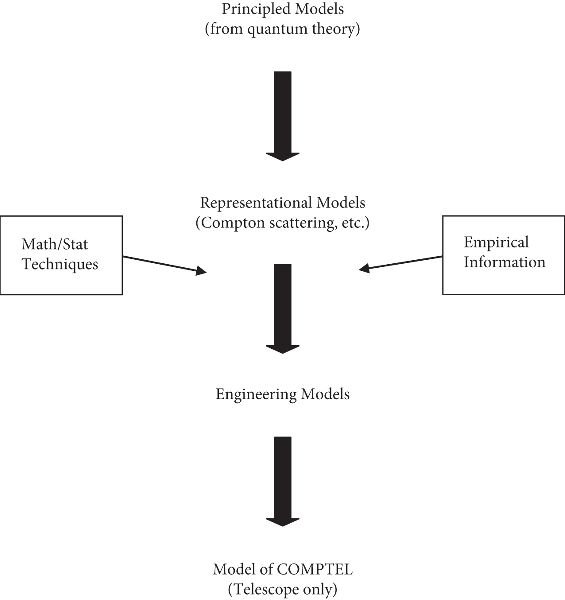
Figure 1.4. A hierarchy of models leading to a model of the instrument.
The most salient output from a COMPTEL experiment is a computer graphic, together with information as to how it is to be read (e.g., the values of a variable associated with color coding). Which is to say, the output is already a model of the data. What would be considered the “raw” data is information about individual gamma ray interactions. This information is recorded, of course, and can be accessed to answer specific questions. But the graphics programming already has built into it algorithms that convert large numbers of individual “hits” into a continuous graphic. Now that philosophers of science have become aware of the importance of distinguishing between data and a model of the data, the actual process of producing a model of the data from the original data has largely become hidden in the design of the hardware and software that are part of the experiment.
Many contemporary experiments, like those involving satellite-based observatories, yield very large data sets—thousands and even millions of individual data points. The resulting data models are thus incredibly rich; they are so rich that that they can serve as good substitutes for the lowest-level theoretical models. In fact, in many instances we do not know enough about the initial conditions to produce a bottom-level theoretical model that could be expected to fit the real system as well as our best data model. This was the case with knowledge of the distribution of gamma ray sources in the center of the Milky Way. It was expected on theoretical grounds that there would be sources of 1.8 MeV gamma rays, but theory, even supplemented with optical examination of the center of the Milky Way, provides little detailed knowledge of the distribution of those sources. The data model thus provides the best representational model we have of this distribution.
THE MAIN CONCLUSIONS are (1) understanding a data model requires having a good model of the experiment, and (2) producing a model of an experiment requires going outside the context of the traditional Suppes hierarchy of models. In particular, it requires consideration of the material, computational, and agential aspects of the experiment. Figure 1.5 is an attempt to capture these conclusions in a single diagram. The horizontal double arrow represents the interpretation of the data in terms of the concepts of the model of the data and the subsequent incorporation of the data into the data model. Finally, the example of the Compton Gamma Ray Telescope suggested several noteworthy features present in many contemporary experiments. (1) The operative output of many experiments is not data, but a data model. The construction of a data model is built into the hardware, with some of the software presumably modifiable as desired. (2) In “data rich” contexts, a data model may function as a representational model. It may effectively be the richest representational model available.
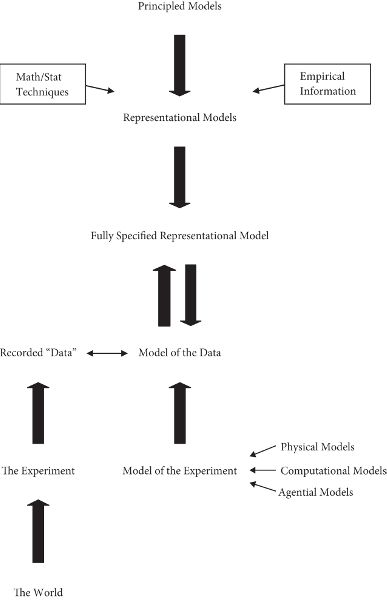
Figure 1.5. A model of an experiment that considers the material, computational, and agential aspects.
Notes
1. I discuss these other possible hierarchies in Giere (2010).
2. For more information about this example, including color reproductions of some data, see Giere (2006), chapter 3.
3. A major exception is Nancy Cartwright (1999), and her earlier works.
4. I elaborated this view of scientific judgment in Giere (1985), reprinted with minor changes in Giere (1999). See also Giere (1988), chapter 6.
5. This view of scientific cognition is elaborated in Giere (2006), chapter 5.
References
Cartwright, Nancy D. 1999. The Dappled World: A Study of the Boundaries of Science. Cambridge: Cambridge University Press.
Franklin, Allan. 1986. The Neglect of Experiment. Cambridge: Cambridge University Press.
Giere, Ronald N. 1985. “Constructive Realism.” In Images of Science, edited by P. M. Churchland and C. A. Hooker, 75–98. Chicago: University of Chicago Press.
Giere, Ronald N. 1988. Explaining Science: A Cognitive Approach. Chicago: University of Chicago Press.
Giere, Ronald N. 1999. Science without Laws. Chicago: University of Chicago Press.
Giere, Ronald N. 2006. Scientific Perspectivism. Chicago: University of Chicago Press.
Giere, Ronald N. 2010. “An Agent-Based Conception of Models and Scientific Representation.” Synthese 172 (2): 269–81.
Hacking, Ian. 1983. Representing and Intervening. Cambridge: Cambridge University Press.
Morgan, Mary, and Margaret Morrison, eds. 1999. Models as Mediators: Perspectives on Natural and Social Science. Cambridge: Cambridge University Press.
Suppes, Patrick. 1962. “Models of Data.” In Logic, Methodology and Philosophy of Science: Proceedings of the 1960 International Conference, edited by E. Nagel, P. Suppes, and A. Tarski, 252–61. Stanford, Calif.: Stanford University Press.