Introduction
Isabelle f. Peschard and Bas C. van Fraassen
The philosophical essays on modeling and experimenting in this volume were originally presented at three workshops on the experimental side of modeling at San Francisco State University in 2009–2011. The debates that began there continue today, and our hope is that they will make a difference to what the philosophy of science will be. As a guide to this collection the introduction will have two parts: an overview of the individual contributions, followed by an account of the historical and methodological context of these studies.
Overview of the Contributions
In this overview we present the individual essays of the collection with a focus on the relations between them and on how they can be read within a general framework for current studies in this area. Thus, first of all, we do not view experiments simply as a tribunal for producing the data against which models are tested, but rather as themselves designed and shaped in interaction with the modeling process. Both the mediating role of models and the model dependence, as well as theory dependence, of measurement come to the fore. And, conversely, the sequence of changing experimental setups in a scientific inquiry will, in a number of case studies, be seen to make a constructive contribution to the process of modeling and simulating. What will be especially evident and significant is the new conception of the role of data not as a given, but as what needs to be identified as what is to be accounted for. This involves normative and conceptual innovation: the phenomena to be investigated and modeled are not precisely identified beforehand but specified in the course of such an interaction between experimental and modeling activity.
It is natural to begin this collection with Ronald Giere’s “Models of Experiments” because it presents the most general, overall schema for the description of scientific modeling and experimenting: a model of modeling, one might say. At the same time, precisely because of its clarity and scope, it leads into a number of controversies taken on by the other participants.
Ron Giere’s construal of the process of constructing and evaluating models centers on the comparison between models of the data and fully specified representational models. Fully specified representational models are depicted as resulting from other models. They are obtained from more general representational models by giving values to all the variables that appear in those models. This part of Giere’s model of the modeling process (briefly, his meta-model) represents the components of a theoretical activity, but it also comprises the insertion of empirical information, the information required to give values to the variables that characterize a specific experimental situation.
Giere’s account gives a rich representation of the different elements that are involved in the activities of producing, on the one hand, theoretical models and, on the other hand, data models. It also makes clear that these activities are neither purely theoretical nor purely empirical.
In Giere’s meta-model, data models are obtained from models of experiments. It should be noted, however, that they are not obtained from models of experiments in the same sense as fully specified representational models are obtained from representational models. Strictly speaking, one should say that data models are obtained from a transformation of what Giere calls “recorded data,” data resulting from measuring activity, which itself results from running an experiment. And these operations also appear in his meta-model. But a model of the experiment is a representation of the experimental setup that produces the data from which the data model is constructed. So data models are obtained from models of experiments in the sense that the model of the experiment presents a source of constraint on what kind of data can be obtained, and thereby a constraint on the data model. It is this constraint that, in Giere’s model of the modeling process, the arrow from the model of the experiment to the data model represents.
Another way to read the relation represented on Giere’s schema between data model and model of the experiment is to see it as indicating that understanding a data model requires understanding the process that produced it, and thereby understanding the model of the experiment.
In the same way as the activity involved in producing theoretical models for comparison with data models is not exclusively theoretical, because it requires the use of empirical information, the activity involved in producing data models is not exclusively empirical. According to Giere, a model of the experiment is a map of the experimental setup that has to include three categories of components: material (representation of the instruments), computational (computational network involved in producing models of the data from instruments’ input), and agential (operations performed by human agents). Running the experiment, from the use of instruments to the transformation of data resulting in the data model, requires a certain understanding of the functioning of the instruments and of the computational analysis of the data which will be, to a variable extent, theoretical.
Because of the generality and large scope of Giere’s meta-model, it leaves open many topics that are taken up later on in the collection. One might find it surprising that the notion of phenomenon does not appear here and wonder where it could be placed. One possibility would be to locate it within “the world.” But in Giere’s meta-model, the world appears as something that is given, neither produced nor constrained by any other component of the modeling process. As we will see in Joseph Rouse’s essay, to merely locate phenomena within the world “as given” betrays the normative dimension that is involved in recognizing something as a phenomenon, which is very different from recognizing something as simply part of the world. What one might find missing also in Giere’s model is the dynamical, interactive relation between the activities that produce theoretical and data models, which is emphasized in Anthony Chemero’s contribution, and again in Michael Weisberg’s. In Giere’s schema, these activities are only related through their product when they are compared. Joe Rouse’s contribution calls that into question as well in his discussion of the role of phenomena in conceptual understanding.
Thus, we see how Giere’s presentation opens the door to a wide range of issues and controversies. In Giere’s schema, the model of the experiment, just like the world, and like phenomena if they are mere components of the world, appears as given. We do not mean, of course, that Giere is oblivious to how the model of the experiment comes about; it is not created ex nihilo. But in this schema it is left aside as yet how it is produced or constrained by other components of the modeling process. It is given, and it is descriptive: a description of the experimental setup. But scientists may be wrong in their judgment that something is a phenomenon. And they may be wrong, or on the contrary show remarkable insight, in their conception of what needs and what does not need to be measured to further our understanding of a certain object of investigation. Arguably, just like for phenomena, and to allow for the possibility of error, the conception of the model of the experiment needs to integrate a normative dimension. In that view, when one offers a model of the experiment, one is not simply offering a description but also making a judgment about what needs to be, what should be, measured. As we will see, the addition of this normative dimension seems to be what most clearly separates Chemero’s from Giere’s approach to the model of the experiment.
In Anthony Chemero’s “Dynamics, Data, and Noise in the Cognitive Sciences,” a model of the experiment is of a more general type than it is for Giere. In Chemero’s sense it is not a specific experimental arrangement but rather a kind of experimental arrangement, defined in terms of what quantities it is able to measure, without specifying the details of what instruments to use or how.
Chemero comes to issues in the philosophy of modeling and its experimental components from the perspective of dynamical modeling in cognitive science. This clear and lucid discussion of dynamical modeling combines with an insightful philosophical reflection on some of the Chemero’s own experimental work. The essay makes two main contributions of particular relevance to our overall topic, both at odds with traditional views on the experimental activity associated with model testing. The first one is to provide a clear counterexample to what Chemero calls “the methodological truism”: “The goal of a good experiment is to maximize primary variance, eliminate secondary variance, and minimize error variance.”
The primary variance is the evolution of the variable of interest, or systematic variance of the dependent variable, under the effect of some other, independent variables that are under control. The secondary variance is the systematic variance of an independent variable resulting from the effect of variables other than the independent variables. The error variance is what is typically referred to as “noise”: unsystematic variance of the dependent variable. The methodological truism asserts, in effect, that noise is not informative and is only polluting the “real” signal, the real evolution of the variable of interest. So it should be minimized and what remains will be washed out by using some measure of the central tendency of the collection of measurements of the dependent variable, such as the mean.
As counterexample to the methodological truism, Chemero presents a case study where the noise is carrying information about the very phenomenon under investigation.
Chemero’s second aim is to illustrate a normative notion of the model of the experiment and, at the same time, to show that to construct a good experimental setup is not just a matter of technical skills but also a matter of determining what quantities to measure to obtain empirical evidence for a target phenomenon. Along the way it is also shown that dynamical models in cognitive science are not simply descriptions of phenomena but fully deserve to be considered as explanations as well.
The case study that Chemero analyzes uses a Haken-Kelso-Bunz model of coordination dynamics. This model has been famously used to model the dynamics of finger wagging, predicting, for instance, that beyond a certain rate only one of two possible behaviors is stable, namely in-phase movement. But it has also been applied to many other topics of study in cognitive science, from neural coordination dynamics to speech production to interpersonal coordination. Chemero discusses the use of this model to investigate the transition described by Heidegger between readiness-to-hand and unreadiness-to-hand: “The dynamical model was used to put Heidegger’s claims about phenomenology into touch with potentially gatherable data.”
Given the project to test Heidegger’s idea of a transition between two forms of interactions with tools—ready-to-hand and unready-to-hand—the challenge was to determine what sort of quantities could serve as evidence for this transition. To determine what the experimental setup needs to be is to offer a model of the experiment. To offer such a model is not just to give a description of experimental arrangements, it is to make a claim about what sort of quantities can serve as evidence for the phenomenon of interest and thus need to be measured. It is a normative claim; and as Rouse’s essay will make clear, it is defeasible. Scientists may come to revise their view about what sorts of quantities characterize a phenomenon—and that is especially so in cognitive science.
The experimenters arrive at a model of the experiment by first interpreting the notion of ready-to-hand in terms of an interaction-dominant system: to be in a ready-to-hand form of interaction with a tool is to form an interaction-dominant system with the tool. This means a kind of system where “the interactions are more powerful than the intrinsic dynamics of the components” and where the components of the system cannot be treated in isolation. An interaction-dominant system exhibits a special variety of fluctuation called 1/f noise or pink noise (“a kind of not-quite-random, correlated noise”), and the experimenters take it that evidence for interaction dominance will be evidence for the ready-to-hand form of interaction.
That is how the methodological truism is contradicted: in that case, noise is not something that is simply altering the informative part of the signal, not something that should be minimized and be compensated for. Instead, it is a part of the signal that is carrying information, information about the same thing that the systematic variation of the primary variable carries information about. As we will see below, Knuuttila and Loettgers make a similar point in their essay in the context of experimental modeling of biological mechanisms.
Interpretation and representation are, it is said, two sides of one coin. St. Elmo’s fire may be represented theoretically as a continuous electric discharge; observations of St. Elmo’s fire provide data that may be interpreted as signs of a continuous electric discharge. To see St. Elmo’s fire as a phenomenon to be modeled as plasma—ionized air—rather than as fire is to see it through the eyes of theory; it is possible only if, in the words of Francis Bacon, “experience has become literate.” But the relation between theory and world is not unidirectional; the phenomena, Joseph Rouse argues in his essay, contribute to conceptual understanding.
Rouse’s contribution addresses the question of what mediates between model and world by focusing on the issue of conceptual understanding. The link between model and world is clarified as the argument unfolds to show that the phenomena play this mediating role. This may be puzzling at first blush: how can the phenomena play a role in conceptual understanding, in the development and articulation of concepts involved in explaining the world with the help of models? According to Rouse both what conceptual articulation consists in, and the role that phenomena play in this articulation, have been misunderstood.
Traditionally viewed, conceptual articulation is a theoretical activity. About the only role that phenomena play in this activity is as that which this activity aims to describe. Phenomena are seen as what theories are about and what data provide evidence for (Bogen and Woodward 1988). When models and world are put in relation with one another, the concepts are already there to be applied and phenomena are already there to be explained. As Rouse says, “[the relation between theory and the world] comes into philosophical purview only after the world has already been conceptualized.” And the aim of experimental activity, from this perspective, is to help determine whether concepts actually apply to the world. Issues related to experimental activity are seen as mainly technical, as a matter of creating the causal conditions prescribed by the concepts and models that we are trying to apply.
Rouse’s move away from this view on conceptual articulation as mainly theoretical, on phenomena as always already conceptualized, and on experimental activity as a technical challenge starts with giving to phenomena the role of mediator between models and world. Phenomena are not some more or less hidden parts of the world that will hopefully, with enough luck and technical skill, be discovered. Instead, they contribute to the conceptual development and articulation through which we make the world’s complexity intelligible.
How do phenomena play this mediating role? First of all, phenomena could not be mediators if they were merely objects of description (or prediction or explanation): “Phenomena show something important about the world, rather than our merely finding something there.” Phenomena’s mediating role starts with and is grounded in the recognition of their significance. The recognition of their significance is not a descriptive, empirical judgment. It is a normative judgment. It is as normative as saying that a person is good, and just as open to revision. The question of whether they are discovered or constructed is pointless. It is like asking whether the meter unit is discovered or constructed. What matters is the normative judgment that makes the one-meter length into a unit. Similarly, with phenomena what matters is the judgment of their significance, that they show something important about the world.
Saying that something is a phenomenon is to make a bet: what we are betting is what is at stake in making this normative judgment. We are betting that it will enable us to see new things that we were not able to see before—new patterns, new regularities. That is the important thing about the world that the phenomenon is taken to show: the possibility of ordering the world in terms similar to it, and to use these terms to create intelligibility, order, and to make some new judgments of similarity and differences, in the same way as we do with the meter unit.
Rouse makes clear that normativity does not imply self-vindication. On the contrary, we may have to recognize that what we took for a phenomenon does not actually show anything important about the world. That is why there is something at stake in judging that something is a phenomenon. There would be nothing at stake if the judgment were not revisable.
So how do phenomena contribute to conceptual articulation? One tempting mistake at this point would be to think that they do so by providing the conditions in which concepts are applied. We cannot reduce a concept to what is happening under some specific conditions. Phenomena may serve as an anchor for concepts, an epicenter, but they point beyond themselves at the larger world, and that is where the domain of application of concepts lies. Once a pattern has been recognized as significant (“outer recognition”), the issue is “how to go on rightly”—that is, how to correctly identify other cases as fitting this same pattern, as belonging to the domain of application of the same concept (“inner recognition”).
Rouse refuses to reduce the domain of application of concepts to the conditions in which phenomena are obtained, but these conditions are important to his story. To understand how phenomena can play a role without becoming a trap, a black hole for concepts that would exhaust their content, we need to introduce the notion of an experimental system. Perhaps the most important aspect of experimental systems is that they belong to a historical and dynamic network of “systematically interconnected experimental capacities.” What matters, in the story of how phenomena contribute to conceptual articulation, “is not a static experimental setting, but its ongoing differential reproduction, as new, potentially destabilizing elements are introduced into a relatively well-understood system.” It is the development of this experimental network that shows how concepts can be applied further and how conceptual domains can be articulated.
Crucially then, in Rouse’s account, in the same way as there is no way to tell in advance how the experimental network will extend, there is no way to tell in advance how concepts will apply elsewhere, how they will extend further. But what is certain is that the concepts that we have make us answerable in their terms to what will happen in the course of the exploration of new experimental domain: “Concepts commit us to more than we know how to say or do.” In some cases, as experimental domains extend, the difficulties may be regarded as conceptually inconsequential, but in other cases they may require a new understanding of the concepts we had, to “conceptually re-organize a whole region of inquiry.”
Tarja Knuuttila and Andrea Loettgers present an exciting and empirically informed discussion of a new form of mediation between models and experiments. Their subject is the use of a new kind of models, synthetic models, which are systems built from genetic material and implemented in a natural cell environment.
The authors offer an in-depth analysis of the research conducted with two synthetic models, the Repressilator and a dual feedback oscillator. In both cases the use of these models led to new insights that could not have been obtained with just mathematical models and traditional experiments on model organisms. The new insights obtained are distinct contributions of intrinsic and extrinsic noise in cell processes in the former case and of an unanticipated robustness of oscillatory regime in the latter.
Elsewhere on the nature of synthetic models, Knuuttila and Loettgers contrast their functioning and use to that of another genetically engineered system, genetically modified Escherichia coli bacteria (Knuuttila and Loettgers 2014). As they explain, this system was used as a measuring system by virtue of its noise-sensing ability. By contrast, the synthetic models are synthetic systems capable of producing a behavior.
After a review of the debate on the similarities and dissimilarities between models and experiments, and using their case study in support, the authors argue that the epistemic function that synthetic models are able to play is due to characteristics they share both with models and with experiments. Thus, the discussion by Knuuttila and Loettgers of synthetic systems sheds a new light on the debate concerning the similarities and dissimilarities between models and experiments. They acknowledge some similarities but highlight certain differences, in particular the limited number of the theoretical model’s components and the specific materiality of the experimental system, on a par with the system under investigation.
What makes the synthetic systems so peculiar is that some of the characteristics they share with models and with experimental systems are those that make models and experiments epistemically dissimilar. What such systems share with models is that by contrast with natural systems they are constructed on the basis of a model—a mathematical model—and their structure only comprises a limited number of interactive components. What they share with experiments is that when placed in natural conditions they are able to produce unanticipated behavior: they start having “a life of their own.” And it is precisely by virtue of this life of their own that they could lead to new insights when their behavior is not as expected.
It may be surprising to think that the construction of a system in accordance with a theoretical model could be seen as something new. After all, experimental systems that are constructed to test a model are constructed according to the model in question. (That is what it is, in Nancy Cartwright’s suggestive phrase, to be a nomological machine.) But the object of investigation and source of insight in the experiments described by Knuuttila and Loettgers are not the behavior of the synthetic model per se but rather its behavior in natural conditions. Such a synthetic system is not a material model, constructed to be an object of study and a source of claims about some other system, of which it is supposed to be a model. The point of the synthetic system is to be placed in natural conditions, and the source of surprise and insight is the way it behaves in such conditions. What these systems then make possible is to see how natural conditions affect the predicted behavior of the model. That is possible because, by contrast with the mathematical model used as a basis to produce it, the synthetic model is made of the same sort of material as appears in those natural conditions. Synthetic models are also different from the better known “model organisms.” The difference is this: whereas the latter have the complexity and opacity of natural systems, the former have the simplicity of an engineered system. Like models and unlike organisms, they are made up of a limited number of components. And this feature, also, as the authors make clear, is instrumental to their innovative epistemic function.
The philosophical fortunes of the concept of causation in the twentieth century could be the stuff of a gripping novel. Russell’s dismissal of the notion of cause in his “Mysticism and Logic” early in the twentieth century was not prophetic of how the century would end. Of the many upheavals in the story, two are especially relevant to the essays here. One was the turn from evidential decision theory to causal decision theory, in which Nancy Cartwright’s “Causal Laws and Effective Strategies” (1979) was a seminal contribution. The other was the interventionist conception of causal models in the work of Glymour, Pearl, and Woodward that, arguably, had become the received view by the year 2000. In the essays by Cartwright and by Jenann Ismael, we will see the implications of this story for both fundamental philosophical categories and practical applications.
Nancy Cartwright addresses the question of what would be good evidence that a given policy will be successful in a given situation. Will the results of implementing the policy in a certain situation serve as a basis to anticipate the results of the implementation in the new situation? Her essay discusses and compares the abilities of experiments and models to provide reliable evidence. Note well that she is targeting a specific kind of experiment—randomized control trial (RCT) experiments—and a specific kind of model: “purpose-built single-case causal models.”
For the results of the implementation of a policy to count as good evidence for the policy’s efficacy, the implementation needs to meet the experimental standards of a well-designed and well-implemented RCT. But even when that is the case, the evidence does not transfer well, according to Cartwright, to a new situation.
A well-designed and well-implemented RCT can, in the best cases, clinch causal conclusions about the effect of the treatment on the population that received the treatment, the study population. That is, if the experiment comprises two populations that can be considered identical in all respects except for receiving versus not receiving the treatment, and if a proper measurement shows an effect in the study population, then the effect can be reliably attributed to the causal effect of the treatment. The question is whether these conclusions, or conclusions about the implementation of a policy in a given situation on a given population, can travel to a new target population/situation.
According to Cartwright, what the results of a RCT can show is that in the specific conditions of the implementation the implementation makes a difference. But it says nothing about the difference it might make in a new situation. For, supposing the implementation was successful, there must be several factors that are contributing, directly or indirectly, in addition to the policy itself, to the success of that implementation. Cartwright calls these factors support factors. And some of these factors may not be present in the new situation or other factors may be present that will hamper the production of the outcome.
One might think that the randomization that governs the selection of the populations in the RCT provides a reliable basis for the generalization of results of the experiment. But all it does, Cartwright says, is ensure that there is no feature that could by itself causally account for the difference in results between the populations. That does not preclude that some features shared by the two populations function as support factors in the study population and made the success of the treatment possible. All that success requires is that some members of the population exhibit these features in such a way as to produce a higher average effect in the study population. Given that we do not know who these members are, we are unable to identify the support factors that made the treatment successful in these individuals.
Cartwright contrasts RCT experiments with what she calls purpose-built single-case causal models. A purpose-built single-case causal model will, at minimum, show what features/factors are necessary for the success of the implementation: the support factors. The most informative, though, will be a model that shows the contribution of the different factors necessary for the success of the implementation of the policy in a given situation/population, which may not be present in the new situation.
It might seem that the purpose-built single-case causal model is, in fact, very general because it draws on a general knowledge we have about different factors. The example that Cartwright specifically discusses is the implementation of a policy aiming to improve learning outcomes by decreasing the size of classes. The implementation was a failure in California whereas it had been successful in Tennessee. The reduction of class size produces a need for a greater number of classrooms and teachers; in California, that meant hiring less qualified teachers and using rooms for classes that had previously been used for learning activities. A purpose-built single-case causal model, says Cartwright, could have been used to study, say, the relationship between quality of teaching and quality of learning outcome. The model would draw on general knowledge about the relationship between quality of teaching and quality of learning outcome, but it would be a single case in that it would only represent the support factors that may or may not be present in the target situation. That maintaining teaching quality while increasing sufficiently the number of teachers would be problematic in California is the sort of fact, she says, that we hope the modeler will dig out to produce the model we must rely on for predicting the outcomes of our proposed policy.
But how, one might wonder, do we evaluate how bad it really is to lower the number of learning activities? How do we determine that the quality of the teaching will decrease to such an extent that it will counteract the benefit of class reduction? How do we measure teaching quality in the first place?
According to Cartwright, we do not “have to know the correct functional form of the relation between teacher quality, classroom quality, class size, and educational outcomes to suggest correctly . . . that outcomes depend on a function that . . . increases as teacher and room quality increase and decreases as class size increases.” Still, it seems important, and impossible in the abstract, to evaluate the extent to which the positive effect expected from class reduction will be hampered by the negative effect expected from a decrease in teachers or room quality or number of learning activities.
Cartwright recognizes that an experiment investigating the effect of the policy on a representative sample of the policy target would be able to tell us what we want to know. But it is difficult to produce, in general, a sample that is representative of a population. And, furthermore, as the California example makes clear, the scale at which the policy is implemented may have a significant effect on the result of the implementation.
Without testing the implementation of the policy itself, can we not think of other, less ambitious experiments that would still be informative? Would it be helpful, for instance, to have some quantitative indication of the difference that learning activities or lack of experience of teachers, alone, makes on learning outcomes? If we can hope to have scientists good enough to produce models that take into account just the right factors, could we not hope to have scientists good enough to conceive of experiments to investigate these factors so as to get clearer on their contribution?
Cartwright takes it that “responsible policy making requires us to estimate as best we can what is in this model, within the bounds of our capabilities and constraints.” But aren’t experiments generally the way in which precisely we try to estimate the contribution of the factors that we expect to have an effect on the evolution of the dependent variable that we are interested in?
Cartwright’s discussion gives good reasons to think that the results of an experiment that is not guided by a modeling process might be of little use beyond showing what is happening in the specific conditions in which it is realized. It is not clear, however, that models without experiment can give us the quantitative information that is required for its being a guide for action and decision.
She notes that “the experiment can provide significant suggestions about what policies to consider, but it is the model that tells us whether the policy will produce the outcome for us.” Experiments may not be able to say, just by themselves, what the support factors are nor whether they are present in the target situation/population. But, it seems they may help a good deal once we have an idea of what the support factors are, to get clearer on how these factors contribute to the production of the effect. And they may even be of help in finding some factors that had not been considered but that do, after all, have an effect.
Jenann Ismael insists that philosophers’ focus on the products of science rather than its practice has distorted specifically the discussion of laws and causality. She begins with a reflection on Bertrand Russell’s skeptical 1914 paper on the notion of cause, which predisposed a whole generation of empiricists against that notion, but Ismael sees the rebirth of the concept of causal modeling as starting with Nancy Cartwright’s 1979 argument that causal knowledge is indispensable in the design of effective strategies.
Russell had argued that the notion of cause plays no role in modern natural science, that it should be abandoned in philosophy and replaced by the concept of a global dynamical law. His guiding example was Newton’s physics, which provided dynamical laws expressed in the form of differential equations that could be used to compute the state of the world at one time as a function of its state at another. Russell’s message that the fundamental nomic generalizations of physics are global laws of temporal evolution is characterized by Ismael as a prevailing mistaken conviction in the philosophy of science during much of the twentieth century.
But, as she recounts, the concept of cause appears to be perfectly respectable in the philosophy of science today. While one might point to the overlap between the new focus on modality in metaphysics, such as in the work of David Lewis, and the attention to this by such philosophers of science as Jeremy Butterfield and Christopher Hitchcock, Ismael sees the turning point in Nancy Cartwright’s placing causal factors at the heart of practical decision making. Cartwright’s argument pertained most immediately to the controversy between causal and evidential decision theory at that time. But it also marks the beginning of the development of a formal framework for representing causal relations in science, completed in the “interventionist” account of causal modeling due to Clark Glymour, Judea Pearl (whom Ismael takes as her main example), and James Woodward.
Does causal information outrun the information generally contained in global dynamical laws? To argue that it does, Ismael focuses on how a complex system is represented as a modular collection of stable and autonomous components, the “mechanisms.” The behavior of each of these is represented as a function, and interventions are local modifications of these functions. The dynamical law for the whole can be recovered by assembling these in a configuration that imposes constraints on their relative variation so as to display how interventions on the input to one mechanism propagate throughout the system. But the same evolution at the global level could be realized through alternative ways of assembling mechanisms, hence it is not in general possible to recover the causal information from the global dynamics.
Causality and mechanism are modal notions, as much as the concept of global laws. The causal realism Ismael argues for involves an insistence on the priority of mechanism over law: global laws retain their importance but are the emergent product of causal mechanisms at work in nature.
Eventually, after all the scientific strife and controversy, we expect to see strong evidence brought to us by science, to shape practical decisions as well as worldviews. But just what is evidence, how is it secured against error, how is it weighed, and how deeply is it indebted for its status to what is accepted as theory? In the process that involves data-generating procedures, theoretical reasoning, model construction, and experimentation, finally leading to claims of evidence, what are the normative constraints? The role of norms and values in experimentation and modeling, in assessment and validation, has recently taken its place among the liveliest and most controversial topics in our field.
Deborah Mayo enters the fray concerning evidential reasoning in the sciences with a study of the methodology salient in the recent “discovery” of the Higgs boson. Her theme and topic are well expressed in one of her subheadings: “Detaching the Inferences from the Evidence.” For as we emphasized earlier, the data are not a given; what counts as evidence and how it is to be understood are what is at issue.
When the results of the Higgs boson detection were made public, the findings were presented in the terminology of orthodox (“frequentist”) statistics, and there were immediate critical reactions by Bayesian statisticians. Mayo investigates this dispute over scientific methodology, continuing her long-standing defense of the former (she prefers the term “error statistical”) method by a careful inquiry into how the Higgs boson results were (or should be) formulated. Mayo sees “the main function of statistical method as controlling the relative frequency of erroneous inferences in the long run.” There are different types of error, which are all possible ways of being mistaken in the interpretation of the data and the understanding of the phenomenon on the basis of the data, such as mistakes about what factor is responsible for the effect that is observed. According to Mayo, to understand how to probe the different components of the experiment for errors—which includes the use of instruments, their manipulation and reasoning, and how to control for errors or make up for them—is part of what it is to understand the phenomenon under investigation.
Central to Mayo’s approach is the notion of severity: a test of a hypothesis H is severe if not only does it produce results that agree with H if H is correct, but it also very likely produces results that do not agree with H if H is not correct. Severe testing is the basis of what Mayo calls “argument from error,” the argument that justifies the experimenter’s trust in his or her interpretation of the data. To argue from error is to argue that a misinterpretation of the data would have been revealed by the experimental procedure.
In the experiments pertaining to the Higgs boson, a statistical model is presented of the detector, within which researchers define a “global signal strength” parameter μ, such that μ = 0 corresponds to the detection of the background only (hypothesis H0), and μ = 1 corresponds to the Standard Model Higgs boson signal in addition to the background (hypothesis H). The statistical test records differences in the positive direction, in standard deviation or sigma units. The improbability of an excess as large as 5 sigma alludes to the sampling distribution associated with such signal-like results or “bumps,” fortified with much cross-checking. In particular, the probability of observing a result as extreme as 5 sigma, under the assumption it was generated by background alone—that is, assuming that H0 is correct—is approximately 1 in 3,500,000.
Can this be summarized as “the probability that the results were just a statistical fluke is 1 in 3,500,000”? It might be objected that this fallaciously applies the probability to H0 itself—a posterior probability of H0. Mayo argues that this is not so.
The conceptual distinctions to be observed are indeed subtle. H0 does not say the observed results are due to background alone, although if H0 were true (about what is generating the data), it follows that various results would occur with specified probabilities. The probability is assigned to the observation of such large or larger bumps (at both sites) on the supposition that they are due to background alone. These computations are based on simulating what it would be like under H0 (given a detector model). Now the inference actually detached from the evidence is something like There is strong evidence for H. This inference does indeed rely on an implicit principle of evidence—in fact, on a variant of the severe or stringent testing requirement for evidence. There are cases, regrettably, that do commit the fallacy of “transposing the conditional” from a low significance level to a low posterior to the null. But in the proper methodology, what is going on is precisely as in the case of the Higgs boson detection. The difference is as subtle as it is important, and it is crucial to the understanding of experimental practice.
Eric Winsberg’s “Values and Evidence in Model-Based Climate Forecasting” is similarly concerned with the relation between evidence and inference, focusing on the role of values in science through a cogent discussion of the problem of uncertainty quantification (UQ) in climate science—that is, the challenging task of attaching a degree of uncertainty to climate models predictions. Here the role of normative decisions becomes abundantly clear.
Winsberg starts from a specific argument for the ineliminable role of social or ethical values in the epistemic endeavors and achievements of science, the inductive risk argument. It goes like this: given that no scientific claim is ever certain, to accept or reject it is to take a risk and to make the value judgment that it is, socially or ethically, worth taking. No stretch of imagination is needed to show how this type of judgment is involved in controversies over whether, or what, actions should be taken on the basis of climate change predictions.
Richard Jeffrey’s answer to this argument was that whether action should be taken on the basis of scientific claims is not a scientific issue. Science can be value-free so long as scientists limit themselves to estimating the evidential probability of their claims and attach estimates of uncertainties to all scientific claims to knowledge. Taking the estimation of uncertainties of climate model predictions as an example, Winsberg shows how challenging this probabilistic program can be, not just technically but also, and even more importantly, conceptually. In climate science, the method to estimate uncertainties uses an ensemble of climate models obtained on the basis of different assumptions, approximations, or parametrizations. Scientists need to make some methodological choices—of certain modeling techniques, for example—and those choices are not, Winsberg argues, always independent of non-strictly-epistemic value judgments. Not only do the ensemble methods rely on presuppositions about relations between models that are clearly incorrect, especially the presupposition that they are all independent or equally reliable, but it is difficult to see how it could be possible to correct them. The probabilistic program cannot then, Winsberg concludes, produce a value-free science because value judgments are involved in many ways in the very work that is required to arrive at an estimation of uncertainty. The ways they are involved make it impossible to trace these value judgments or even to draw a clear line between normative and epistemic judgments. What gets in the way of drawing this line, in the case of climate models, is that not only are they complex objects, with different parts that are complex and complexly coupled, but they also have a complex history.
Climate models are a result of a series of methodological choices influencing “what options will be available for solving problems that arise at a later time” and, depending on which problems will arise, what will be the model’s epistemic successes or failures. What Joseph Rouse argues about concepts applies here to methodological choices: we do not know what they commit us to. This actual and historical complexity makes it impossible to determine beforehand the effects of the assumptions and choices involved in the construction of the models. For this very reason, the force of his claims, Winsberg says, will not be supported by a single, specific example of value judgment that would have influenced the construction or assessment of climate models. His argument is not about some value judgments happening here or there; it is about how pervasive such judgments are, and about their “entrenchment”—their being so intimately part of the modeling process that they become “mostly hidden from view . . . They are buried in the historical past under the complexity, epistemic distributiveness, and generative entrenchment of climate models.”
While Winsberg’s essay focuses on the interplay of values and criteria in the evaluation of models in climate science, Michael Weisberg proposes a general theory of model validation with a case study in ecology.
What does it mean that a model is good or that one model is better than another one? Traditional theories of confirmation are concerned with the confirmation of claims that are supposed to be true or false. But that is exactly why they are not appropriate, Michael Weisberg argues, for the evaluation of idealized models—which are not, and are not intended to be, truthful representations of their target. In their stead, Weisberg proposes a theory of model validation.
Weisberg illustrates this problem of model evaluation with two models in contemporary ecology. They are models of a beech forest in central Europe that is composed of regions with trees of various species, sizes, and ages. The resulting patchy pattern of the forest is what the models are supposed to account for. Both models are cellular automata: an array of cells that represents a patch of forest of a certain kind and a set of transition rules that, step by step, take each of the cells from one state to another. The transition rules determine at each step what each cell represents based on what the cell and the neighboring cells represented at the previous step. One of the models is more sophisticated than the other: the representation and transition rules take into account a larger number of factors that characterize the forest (e.g., the height of the trees). It is considered a better model than the other one, but it is still an idealization; and the other one, in spite of its being simpler, is nevertheless regarded as at least partially validated and also explanatory.
Weisberg’s project is to develop an account of model validation that explains the basis on which a model is evaluated and what makes one model better than another one. His account builds on Ronald Giere’s view that it is similarities between models and real systems that make it possible for scientists to use models to represent real systems. Following Giere, Weisberg proposes to understand the validation of models as confirmation of theoretical hypotheses about the similarity between models and their intended targets. Weisberg’s account also follows Giere in making the modeler’s purpose a component of the evaluation of models: different purposes may require different models of the same real system and different forms of similarities between the model and the target.
In contrast to Giere, who did not propose an objective measure of similarity, Weisberg’s account does. The account posits a set of features of the model and the target, and Weisberg defines the similarity of a model to its target as “a function of the features they share, penalized by the features they do not share”; more precisely, “it is expressed as a ratio of shared features to non-shared features.” Weisberg’s account is then able to offer a more precise understanding of “scientific purpose.” For example, if the purpose is to build a causal model then the model will need to share the features that characterize the mechanism producing the phenomenon of interest. If the purpose includes simplicity, the modeler should minimize in the model the causal features that are not in the target. By contrast, if the purpose is to build a “how-possible” model, what matters most is that the model shares the static and dynamic features of the target. The way in which the purpose influences the evaluation appears in the formula through a weighting function that assigns a weight to the features that are shared and to those that are not shared. The weight of these features expresses how much it matters to the modeler that these features are shared or not shared and determines the way in which their being shared or not shared influences the evaluation.
This account enables Weisberg to explain why it may not be possible to satisfy different purposes with a single model and why some trade-offs might be necessary. It also enables him to account for what makes, given a purpose, one model better than another one.
And it enables him to account for another really important and neglected aspect of modeling and model evaluation: its iterative aspect. As we saw, the formula includes a weighting function that ascribes weights to the different features to express their relative importance. The purpose of the modeler indirectly plays a role in determining the weighting function in that it determines what the model needs to do. But what directly determines, given the purpose, what the weighting function has to be is some knowledge about what the model has to be like in order to do what the purpose dictates. In some cases, this knowledge will be theoretical: to do this or that the model should have such and such features and should not or does not need to have such and such other features. In some cases, however, Weisberg points out, there will be no theoretical basis to determine which features are more important. Instead, the weights may have to be iteratively adjusted on the basis of a comparison between what the model does and the empirical data that need to be accounted for, until the model does what it is intended to do. That will involve a back and forth between the development of the model and the comparison with the data.
Weisberg speaks here of an interaction between the development of the model and the collection of data. Such an interaction suggests that the development of the model has an effect on the collection of the data. It is an effect that is also discussed in other contributions (Chemero, Knuuttila and Loettgers, and Rouse). It is not clear, at first, how that would happen under Weisberg’s account because it seems to take the intended target, with its features, and the purpose for granted in determining the appropriate validation formula. But it does not need to do so. The model may suggest new ways to investigate the target, for example, by looking for some aspects of the phenomenon not yet noticed but predicted by the model. Finally, Weisberg discusses the basis on which a validated model can be deemed a reliable instrument to provide new results.
In addition to the validation of the model, what is needed, Weisberg explains, is a robustness analysis that shows that the results of the model are stable through certain perturbations. The modelers generally not only want the model to provide new results about the target it was tested against but also want these results to generalize to similar targets. Weisberg does not seem to distinguish between these expectations here. In contrast, Cartwright’s essay makes clear that to project the results of a model for one situation to a new situation may require much more than a robustness analysis.
Symposium on Measurement
Deborah Mayo rightly refers to measurement operations as data-generating procedures. But a number or text or graphics generating procedure is not necessarily generating data: what counts as data, as relevant data, or as evidence, depends on what is to be accounted for in the relevant experimental inquiry or to be represented in the relevant model. If a specific procedure is a measurement operation then its outcomes are values of a specific quantity, but whether there is a quantity that a specific procedure measures, or which quantity that is, and whether it is what is represented as that quantity in a given model, is generally itself what is at stake.
In this symposium, centering on Paul Teller’s “Measurement Accuracy Realism,” the very concept of measurement and its traditional understanding are subjected to scrutiny and debate.
Van Fraassen’s introduction displays the historical background in philosophy of science for the changing debates about measurement, beginning with Helmholtz in the nineteenth century. The theory that held center stage in the twentieth was the representational theory of measurement developed by Patrick Suppes and his coworkers. Its main difficulties pertained to the identification of the quantities measured. The rival analytic theory of measurement proposed by Domotor and Batitsky evades this problem by postulating the reality of physical quantities of concern to the empirical sciences. Both theories are characterized, according to van Fraassen, by the sophistication of their mathematical development and paucity of empirical basis. It is exactly the problem of identifying the quantities measured that is the target of Paul Teller’s main critique, which goes considerably beyond the traditional difficulties that had been posed for those two theories of measurement.
First of all, Teller challenges “traditional measurement-accuracy realism,” according to which there are in nature quantities of which concrete systems have definite values. This is a direct challenge to the analytic theory of measurement, which simply postulates that. But the identification of quantities through their pertinent measurement procedures, on which the representationalist theory relied, is subject to a devastating critique of the disparity between, on the one hand, the conception of quantities with precise values, and on the other, what measurement can deliver. The difficulties are not simply a matter of limitations in precision, or evaluation of accuracy. They also derive from the inescapability of theory involvement in measurement. Ostensibly scientific descriptions refer to concrete entities and quantities in nature, but what are the referents if those descriptions can only be understood within their theoretical context? A naïve assumption of truth of the theory that supplies or constitutes the context might make this question moot, but that is exactly the attitude Teller takes out of play. Measurement is theory-laden, one might say, but laden with false theories! Teller argues that the main problems can be seen as an artifact of vagueness, and applies Eran Tal’s robustness account of measurement accuracy to propose ways of dealing, with vagueness and idealization, to show that the theoretical problems faced by philosophical accounts of measurement are not debilitating to scientific practice.
In his commentary, van Fraassen insists that the identification of physical quantities is not a problem to be evaded. The question raised by Teller, how to identify the referent of a quantity term, is just the question posed in “formal mode” of what it means for a putative quantity to be real. But the way in which this sort of question appears in scientific practice does not answer to the sense it is given in metaphysics. It is rather a way of raising a question of adequacy for a scientific theory which concerns the extent to which values of quantities in its models are in principle determinable by procedures that the theory itself counts as measurements. On his proposal, referents of quantity terms are items in, or aspects of, theoretical models, and the question of adequacy of those models vis à vis data models replaces the metaphysical question of whether quantity terms have real referents in nature.
In his rejoinder, Paul Teller submits that van Fraassen’s sortie to take metaphysics by the horns does not go far enough, the job needs to be completed. And that requires a pragmatist critique. As to that, Teller sees van Fraassen’s interpretation of his, Teller’s, critique of traditional measurement accuracy realism as colored by a constructive empiricist bias. Thus his rejoinder serves to do several things: to rebut the implied criticism in van Fraassen’s comments and to give a larger-scale overview of the differences between the pragmatist and empiricist approaches to understanding science. New in this exchange is Teller’s introduction of a notion of adoption of statements and theories, that has some kinship to van Fraassen’s notion of acceptance of theories but is designed to characterize epistemic or doxastic attitudes that do not involve full belief at any point.
The Historical and Methodological Context
While experimentation and modeling were studied in philosophy of science throughout the twentieth century, their delicate entanglement and mutuality has recently come increasingly into focus. The essays in this collection concentrate on the experimental side of modeling, as well as, to be sure, the modeling side of experimentation.
In order to provide adequate background to these essays, we shall first outline some the historical development of this philosophical approach, and then present in very general terms a framework in which we understand this inquiry into scientific practice. This will be illustrated with case studies in which modeling and experimentation are saliently intertwined, to provide a touchstone for the discussions that follow.
A Brief History
Philosophical views of scientific representation through theories and models have changed radically over the past century.
Early Twentieth Century: The Structure of Scientific Theories
In the early twentieth century there was a rich and complex interplay between physicists, mathematicians, and philosophers stimulated by the revolutionary impact of quantum theory and the theory of relativity. Recent scholarship has illuminated this early development of the philosophy of science in interaction with avant-garde physics (Richardson 1997; Friedman 1999; Ryckman 2005) but also with revolutionary progress in logic and the foundations of mathematics.
After two decades of seminal work in the foundations of mathematics, including the epochal Principia Mathematica (1910–13) with Alfred North Whitehead, Bertrand Russell brought the technique of logical constructs to the analysis of physics in Our Knowledge of the External World (1914) and The Analysis of Matter (1927). Instants and spatial points, motion, and indeed the time and space of physics as well as their relations to concrete experience were subjected to re-creation by this technique. This project was continued by Rudolf Carnap in his famous Der logische Aufbau der Welt (1928) and was made continually more formal, more and more a part of the subject matter of mathematical logic and meta-mathematics. By midcentury, Carnap’s view, centered on theories conceived of as sets of sentences in a formally structured language supplemented with relations to observation and measurement, was the framework within which philosophers discussed the sciences. Whether aptly or inaptly, this view was seen as the core of the logical positivist position initially developed in the Vienna Circle. But by this time it was also seen as contestable. In a phrase clearly signaling discontent, in the opening paragraphs of his “What Theories Are Not” (Putnam 1962), Hilary Putnam called it “the Received View.”
It is not perhaps infrequent that a movement reaches its zenith after it has already been overtaken by new developments. We could see this as a case in point with Richard Montague’s “Deterministic Theories” (Montague 1957), which we can use to illustrate both the strengths and limitations of this approach. Montague stays with the received view of theories as formulated in first-order predicate languages, but his work is rich enough to include a fair amount of mathematics. The vocabulary’s basic expressions are divided, in the Carnapian way, into abstract constants (theoretical terms) and elementary constants (observational terms), with the latter presumed to have some specified connection to scientific observation procedures.
With this in hand, the language can provide us with sufficiently complete descriptions of possible trajectories (“histories”) of a system; Montague can define: “A theory T is deterministic if any two histories that realize T, and are identical at a given time, are identical at all times. Second, a physical system (or its history) is deterministic exactly if its history realizes some deterministic theory.” Although the languages considered are extensional, the discussion is clearly focused on the possible trajectories (in effect, alternative possible “worlds”) that satisfy the theory. Montague announces novel results, such as a clear disconnection between periodicity and determinism, contrary to their intimate relationship as depicted in earlier literature.
But it is instructive to note how the result is proved. First of all, by this definition, a theory that is satisfied only by a single history is deterministic—vacuously, one might say—even if that history is clearly not periodic. Second, given any infinite cardinality for the language, there will be many more periodic systems than can be described by theories (axiomatizable sets of sentences) in that language, and so many of them will not be deterministic by the definition.
Disconcertingly, what we have here is not a result about science, in and by itself, so to speak, but a result that is due to defining determinism in terms of what can be described in a particular language.
Mid-Twentieth Century: First Focus on Models Rather Than Theories
Discontent with the traditional outlook took several forms that would have lasting impact on the coming decades, notably the turn to scientific realism by the Minnesota Center for the Philosophy of Science (Wilfrid Sellars and Grover Maxwell) and the turn to the history of science that began with Thomas Kuhn’s The Structure of Scientific Revolutions (1962), which was first published as a volume in the International Encyclopedia of Unified Science. Whereas the logical positivist tradition had viewed scientific theoretical language as needing far-reaching interpretation to be understood, both these seminal developments involved viewing scientific language as part of natural language, understood prior to analysis.
But the explicit reaction that for understanding scientific representation the focus had to be on models rather than on a theory’s linguistic formulation, and that models had to be studied independently as mathematical structures, came from a third camp: from Patrick Suppes, with the slogan “mathematics, not meta-mathematics!” (Suppes 1962, 1967).
Suppes provided guiding examples through his work on the foundations of psychology (specifically, learning theory) and on physics (specifically, classical and relativistic particle mechanics). In each case he followed a procedure typically found in contemporary mathematics, exemplified in the replacement of Euclid’s axioms by the definition of Euclidean spaces as a class of structures. Thus, Suppes replaced Newton’s laws, which had been explicated as axioms in a language, by the defining conditions on the set of structures that count as Newtonian systems of particle mechanics. To study Newton’s theory is, in Suppes’s view, to study this set of mathematical structures.
But Suppes was equally intent on refocusing the relationship between pure mathematics and empirical science, starting with his address to the 1960 International Congress on Logic, Methodology, and Philosophy of Science, “Models of Data” (Suppes 1962). In his discussion “Models versus Empirical Interpretations of Theories” (Suppes 1967), the new focus was on the relationship between theoretical models and models of experiments and of data gathered in experiments. As he presented the situation, “We cannot literally take a number in our hands and apply it to a physical object. What we can do is show that the structure of a set of phenomena under certain empirical operations is the same as the structure of some set of numbers under arithmetical operations and relations” (Suppes 2002, 4). Then he introduced, if still in an initial sketch form, the importance of data models and the hierarchy of modeling activities that both separate and link the theoretical models to the practice of empirical inquiry:
The concrete experience that scientists label an experiment cannot itself be connected to a theory in any complete sense. That experience must be put through a conceptual grinder . . . [Once the experience is passed through the grinder,] what emerges are the experimental data in canonical form. These canonical data constitute a model of the results of the experiment, and direct coordinating definitions are provided for this model rather than for a model of the theory . . . The assessment of the relation between the model of the experimental results and some designated model of the theory is a characteristic fundamental problem of modern statistical methodology. (Suppes 2002, 7)
While still in a “formal” mode—at least as compared with the writings of a Maxwell or a Sellars, let alone Kuhn—the subject has clearly moved away from preoccupation with formalism and logic to be much closer to the actual scientific practice of the time.
The Semantic Approach
What was not truly possible, or advisable, was to banish philosophical issues about language entirely from philosophy of science. Suppes offered a correction to the extremes of Carnap and Montague, but many issues, such as the character of physical law, of modalities, possibilities, counterfactuals, and the terms in which data may be presented, would remain. Thus, at the end of the sixties, a via media was begun by Frederick Suppe and Bas van Fraassen under the name “the Semantic Approach” (Suppe 1967, 1974, 2000; van Fraassen 1970, 1972).
The name was perhaps not quite felicitous; it might easily suggest either a return to meta-mathematics or alternatively a complete banishing of syntax from between the philosophers’ heaven and earth. In actuality it presented a focus on models, understood independently of any linguistic formulation of the parent theory but associated with limited languages in which the relevant equations can be expressed to formulate relations among the parameters that characterize a target system.
In this approach the study of models remained closer to the mathematical practice found in the sciences than we saw in Suppes’s set-theoretic formulations. Any scientist is thoroughly familiar with equations as a means of representation, and since Galois it has been common mathematical practice to study equations by studying their sets of solutions. When Tarski introduced his new concepts in the study of logic, he had actually begun with a commonplace in the sciences: to understand an equation is to know its set of solutions.
As an example, let us take the equation x2 + y2 = 2, which has four solutions in the integers, with x and y able to take either values +1 or −1. Reifying the solutions, we can take them to be the sequences <+1, +1>, <−1, +1>, <+1, −1>, and <−1, −1>. Tarski would generalize this and give it logical terminology: these sequences satisfy the sentence “x2 + y2 = 2.” So when Tarski assigned sets of sequences of elements to sentences as their semantic values, he was following that mathematical practice of characterizing equations through their sets of solutions. It is in this fashion that one arrives at what in logical terminology is a model. It is a model of a certain set of equations if the sequences in the domain of integers, with the terms’ values as specified, satisfy those equations. The set of all models of the equations, so understood, is precisely the set of solutions of those equations.[1]
The elements of a sequence that satisfy an equation may, of course, not be numbers; they may be vectors or tensors or scalar functions on a vector space, and so forth. Thus, the equation picks out a region in a space to which those elements belong—and that sort of space then becomes the object of study. In meta-mathematics this subject is found more abstractly: the models are relational structures, domains of elements with relations and operations defined on them. Except for its generality, this does not look unfamiliar to the scientist. A Hilbert space with a specific set of Hermitean operators, as a quantum-mechanical model, is an example of such a relational structure.
The effect of this approach to the relation between theories and models was to see the theoretical models of a theory as clustered in ways natural to a theory’s applications. In the standard example of classical mechanics, the state of a particle is represented by three spatial and three momentum coordinates; the state of an N-particle system is thus represented by 3N spatial and 3N momentum coordinates. The space for which these 6N-tuples are the points is the phase space common to all models of N-particle systems. A given special sort of system will be characterized by conditions on the admitted trajectories in this space. For example, a harmonic oscillator is a system defined by conditions on the total energy as a function of those coordinates. Generalizing on this, a theory is presented through the general character of a “logical space” or “state space,” which unifies its theoretical models into families of models, as well as the data models to which the theoretical models are to be related, in specific ways.
Reaction: A Clash of Attitudes and a Different Concept of Modeling
After the death of the Received View (to use Putnam’s term), it was perhaps the semantic approach, introduced at the end of the 1960s, that became for a while the new orthodoxy, perhaps even until its roughly fiftieth anniversary (Halvorson 2012, 183). At the least it was brought into many areas of philosophical discussion about science, with applications extended, for example, to the philosophy of biology (e.g., Lloyd 1994). Thomas Kuhn exclaimed, in his outgoing address as president of the Philosophy of Science Association, “With respect to the semantic view of theories, my position resembles that of M. Jourdain, Moliere’s bourgeois gentilhomme, who discovered in middle years that he’d been speaking prose all his life” (1992, 3).
But a strong reaction had set in about midway in the 1980s, starting with Nancy Cartwright’s distancing herself from anything approaching formalism in her How the Laws of Physics Lie: “I am concerned with a more general sense of the word ‘model.’ I think that a model—a specially prepared, usually fictional description of the system under study—is employed whenever a mathematical theory is applied to reality, and I use the word ‘model’ deliberately to suggest the failure of exact correspondence” (Cartwright 1983, 158–59). Using the term “simulacra” to indicate her view of the character and function of models, she insists both on the continuity with the semantic view and the very different orientation to understanding scientific practice:
To have a theory of the ruby laser [for example], or of bonding in a benzene molecule, one must have models for those phenomena which tie them to descriptions in the mathematical theory. In short, on the simulacrum account the model is the theory of the phenomenon. This sounds very much like the semantic view of theories, developed by Suppes and Sneed and van Fraassen. But the emphasis is quite different. (Cartwright 1983, 159)
What that difference in emphasis leads to became clearer in her later writings, when Cartwright insisted that a theory does not just arrive “with a belly-full” of models. This provocative phrasing appeared in a joint paper in the mid-1990s, where the difference between the received view and the semantic approach was critically presented:
[The received view] gives us a kind of homunculus image of model creation: Theories have a belly-full of tiny already-formed models buried within them. It takes only the midwife of deduction to bring them forth. On the semantic view, theories are just collections of models; this view offers then a modern Japanese-style automated version of the covering-law account that does away even with the midwife. (Cartwright, Shomar, and Suárez 1995, 139)
According to Cartwright and her collaborators, the models developed in application of a theory draw on much that is beside or exterior to that theory, and hence not among whatever the theory could have carried in its belly.
What is presented here is not a different account of what sorts of things models are, but rather a different view of the role of theories and their relations to models of specific phenomena in their domain of application. As Suárez (1999) put it, their slogan was that theories are not sets of models, they are tools for the construction of models. One type of model, at least, has the traditional task of providing accurate accounts of target phenomena; these they call representative models. They maintain, however, that we should not think of theories as in any sense containing the representative models that they spawn. Their main illustration is the London brothers’ model of superconductivity. This model is grounded in classical electromagnetism, but that theory only provided tools for constructing the model and was not by itself able to provide the model. That is, it would not have been possible to just deduce the defining equations of the model in question after adding data concerning superconductivity to the theory.[2]
Examples of this are actually ubiquitous: a model of any concretely given phenomenon will represent specific features not covered in any general theory, features that are typically represented by means derived from other theories or from data.[3]
It is therefore important to see that the turn taken here, in the philosophical attention to scientific modeling in practice, is not a matter of logical dissonance but of approach or attitude, which directs how a philosopher’s attention selects what is important to the understanding of that practice. From the earlier point of view, a model of a theory is a structure that realizes (satisfies) the equations of that theory, in addition to other constraints. Cartwright and colleagues do not present an account of models that contradicts this. The models constructed independently of a theory, to which Cartwright and colleagues direct our attention, do satisfy those equations—if they did not, then the constructed model’s success would tend to refute the theory. The important point is instead that the process of model construction in practice was not touched on or illuminated in the earlier approaches. The important change on the philosophical scene that we find here, begun around 1990, is the attention to the fine structure of detail in scientific modeling practice that was not visible in the earlier more theoretical focus.[4]
Tangled Threads and Unheralded Changes
A brief history of this sort may give the impression of a straightforward, linear development of the philosophy of science. That is misleading. Just a single strand can be followed here, guided by the need to locate the contributions in this volume in a fairly delineated context. Many other strands are entangled with it. We can regard David Lewis as continuing Carnap’s program of the 1970s and 1980s (Lewis 1970, 1983; for critique see van Fraassen 1997). Equally, we can see Hans Halvorson as continuing in as well as correcting the semantic approach in the twenty-first century (Halvorson 2012, 2013; for discussion see van Fraassen 2014a). More intimately entangled with the attention to modeling and experimenting in practice are the writings newly focused on scientific representation (Suárez 1999, 2003; van Fraassen 2008, 2011). But we will leave aside those developments (as well as much else) to restrict this chapter to a proper introduction to the articles that follow. Although the philosophy of science community is by no means uniform in either focus or approach, the new attitude displayed by Cartwright did become prevalent in a segment of our discipline, and the development starting there will provide the context for much work being done today.
Models as Mediators
The redirection of attention to practice thus initiated by Cartwright and her collaborators in the early 1990s was systematically developed by Morgan and Morrison in their contributions to their influential collection Models as Mediators (1999). Emphasizing the autonomy and independence of theory, they describe the role or function of models as mediating between theory and phenomena.
What, precisely, is the meaning of this metaphor? Earlier literature typically assumed that in any scientific inquiry there is a background theory, of which the models constructed are, or are clearly taken to be, realizations. At the same time, the word “of” looks both ways, so to speak: those models are offered as representations of target phenomena, as well as being models of a theory in whose domain those phenomena fall. Thus, the mediation metaphor applies there: the model sits between theory and phenomenon, and the bidirectional “of” marks its middle place.
The metaphor takes on a stronger meaning with a new focus on how models may make their appearance, to represent experimental situations or target phenomena, before there is any clear application of, let alone derivation from, a theory. A mediator effects, and does not just instantiate, the relationship between theory and phenomenon. The model plays a role (1) in the representation of the target, but also (2) in measurements and experiments designed to find out more about the target, and then farther down the line (3) in the prediction and manipulation of the target’s behavior.
Morrison and Morgan’s account (Morrison 1999; Morrison and Morgan 1999) begins with the earlier emphasis on how model construction is not derivation from a theory but construction that draws on theory, on data, on other theories, on guiding metaphors, on a governing paradigm. That is the main content of the first thesis: independence in construction. The second thesis, autonomy of models, to the extent that it goes beyond this independence, can be illustrated by the delay, even negligence, with respect to the task of showing that the model proposed for a given phenomenon does actually satisfy the basic equations of the main theory.
For example, in fluid mechanics the basic principle in the background of all theorizing and model construction is the set of Navier–Stokes equations. There is no sense in which a specific fluid mechanics model, such as a model of turbulence in the wake of an obstacle, was ever deduced from those equations alone. But there is so little suspicion that a given model, proposed in practice, violates those equations that eventual checking on the consistency is left to mathematicians, without the experimenter waiting for reassurance. Morrison illustrates the point with Ludwig Prandtl’s 1904 construction of a model of the boundary layer model for viscous fluids. His construction employs the tools of classical hydrodynamics and the Navier–Stokes equations, but “the important point is that the approximations used in the solutions come not from a direct simplification of the mathematics of the theory, but from the phenomenology of the fluid flow as represented in the model” (Morrison, 1999, 59).
That models are autonomous and independent in this sense does not by itself reveal the character of the role of mediation. The term “mediator” connotes a bridging of some sort between two disparate sides in a dialogue, dispute, or collaboration. So it is crucial to appreciate the two sides: while theories are drawn on to construct models, conversely the models aid in theory construction. In particular cases, a model may come along first, the extension of theory following upon what was learned while a resistant phenomenon was being modeled. That models function as mediators between theory and the phenomena implies then that modeling can enter in two ways. The process of modeling may start with a phenomenon (physical system or process) and draw on theory to devise a representation of that phenomenon; or it may start with a theory, draw on other sources such as data or auxiliary theories to compliment that theory, and introduce as model a structure satisfying that theory. In the first case it is (or is intended to be) an accurate representation of a phenomenon; in the second case it is a representation of what the theory depicts as going on in phenomena of this sort.
As is typical of metaphors, drawing out the content of “models mediate between theory and phenomena” turns out to be a complex but instructive exercise.
Recent Developments
As in science, so in philosophy: practice goes far beyond what is preached. By the second decade of the twenty-first century, in which the present collection is situated, the previous developments had borne ample fruit. In two new series of conferences, Models and Simulations and The Society for Philosophy of Science in Practice, starting, respectively, in France in 2006 and in the Netherlands in 2007, the new orientation to scientific practice has been saliently displayed. Of signal importance in the work by Nancy Cartwright, Mary Morgan, Margaret Morrison, Mauricio Suárez, and the participants in these conferences was the detailed examination of actual scientific practice in experimentation and modeling.
More or less concurrently with the workshops of 2009–2011, a bevy of new studies appeared on how computer simulation was changing conceptions of modeling, measurement, and experiment. These included works by our contributors Ronald Giere (2009), Isabelle Peschard (2011b, 2012, 2013), Michael Weisberg (2013), Eric Winsberg (2009, 2010), and by, for example, Anouk Barberousse, Sara Franceschelli, and Cyrille Imbert (2009), Paul Humphreys (2004), Margaret Morrison (2009), E. C. Parke (2014), and Wendy Parker (2009). The main issue about computer simulation, evoking sustained debate in the literature, was saliently expressed by Margaret Morrison: Do computer simulations ever have the same epistemic status as experimental measurement? Morrison had argued earlier (as we have seen) that models function, in some sense, as measuring instruments; she now argued that there is a way in which simulation can be said to constitute an experimental activity (see further Morrison 2015).
At the same time, as debated in the workshops, there were new arguments concerning the theory-dependence of measurement. This surfaces in the present collection especially in the contributions by Joseph Rouse and Paul Teller, but such discussion continued in a series of publications subsequently: Ann-Sophie Barwich and Hasok Chang (2015), Nancy Cartwright (2014), Teru Miyake (2013, 2015), Eran Tal (2011, 2012, 2013), and Bas van Fraassen (2012, 2014b).
At issue here are the roles of idealization, abstraction, and prediction in establishing measurement outcomes as well as the theoretical status of criteria to determine what counts as a measurement and what it is that is measured. A special issue of Studies in the History and Philosophy of Science, Part A (vol. 65–66, October–December 2017) is dedicated to the history and philosophy of measurement in relation to modeling and experimentation.
Experimentation and Modeling: A Delicate Entanglement
In the remainder of this introduction we will sketch in broad outlines, with illustrative case studies, a framework in which we see the experimental side of modeling currently approached.[5]
As the philosophical take on modeling changed, so did views of how experimentation relates to modeling. The earlier stages inherited the logical positivist view of experimentation as the tribunal that tests models against data delivered by experimental and observational outcomes. In later stages much attention was paid to how measurement itself involves modeling from the outset.[6]
There is, as might be expected, another side to the coin as well: that, conversely, experimental activity makes a constructive contribution to the processes of modeling and simulating. The autonomy of modeling was a new theme that is to be conjoined with another new theme: the constructive relation of experimentation to modeling as an interactive, creative, open-ended process that modifies both along the way.
There are two aspects to this interaction. The first is that the specification of the relevant parameters of a phenomenon are not given from the outset. The phenomenon vaguely defined at the beginning of the investigation needs to be specified, and this is done by specifying what data represent the phenomenon and what data are to be regarded as a manifestation of the phenomenon. What needs to be settled through experimentation will then include the conditions in which measurement outcomes qualify as relevant data—that is, data to which a putative model of the phenomenon is accountable. The second, which follows upon this, is conceptual innovation, as a result of an effort to make sense, through modeling, of the phenomenon and the conditions of its occurrence.
Looking back from our present vantage point we may discern illustrative examples in the past: surely it was experimentation that led to the reconceptualization of lightning as electric discharge, for example. But the intricate ballet between experimental and modeling progress can only become clear through a detailed analysis, and for this we shall choose a case in fluid mechanics.
Example of a Phenomenon: Formation of a Wake
The formation of a wake is a very common phenomenon that happens when air or liquid goes over a bluff (not streamlined) body, which can be a pole, a rock, or an island. The work on a better theoretical understanding of wakes spread from meteorology to the stability of bridges or platforms, from the design of cars and airplane wings to that of helicopter vanes—and more generally to all cases where periodic instabilities or transitions toward chaotic behavior are possible.
A simple physical model of this phenomenon in a laboratory can show the wake of a flow behind a cylinder when the velocity of the upstream flow reaches a certain critical value. In a diagram such a flow going, say, from left to right can be visualized in the plane perpendicular to the axis of the cylinder, with the wake formed by vortices that are emitted alternatively on each side of the cylinder and carried away with the downstream flow.
As simple as it may look, the attempt to construct a theoretical model of this sort of wake triggered an enormous number of studies, and no less controversy. As our main example from this literature let us take one, seemingly simple, question that was the object of a debate involving experimental as well as numerical and theoretical studies in fluid mechanics in the second half of the twentieth century.
Formulation of such a question begins inevitably within a pre-existing modeling tradition. The system is initially characterized in terms of three quantities: the velocity (U) upstream of the flow, the diameter (d) of the cylinder, and the viscosity (ν) of the fluid. The most significant quantity, defined in terms of these three, is the dimensionless Reynolds number (Re):
Re = Ud/ν
The wake is formed when this number reaches a critical value, where vortices are emitted with a certain frequency, the shedding frequency.
Question: What happens when Re is increased within a certain interval beyond the critical value?
How does the evolution of the shedding frequency of the vortices vary with Re? Specifically, as Re is increased within a certain interval beyond the critical value is the variation with the Re of the shedding frequency a continuous linear variation or is there some discontinuity?
The question can itself arise only within a theoretical background, but it clearly asks for data from experiment before models of the formation of the wake can be assessed and also, in effect, before a suitable model of the entire phenomenon can be constructed.
Origin of the Controversy: The Discontinuity
A detailed experimental study of the wake appeared in 1954 with the publication of Anatol Roshko’s dissertation “On the Development of Turbulent Wakes from Vortex Streets.” The experimental results showed that in the range (40–150) of Re “regular vortex sheets are formed and no turbulent motion is developed.” This is called the stable range. Between Re = 150 and Re = 300 turbulent velocity fluctuations accompany the periodic formation of vortices: this is the range of turbulence. For the stable range Roshko provided an empirical formula for the increase of shedding frequency of velocity: a linear variation of the shedding frequency with the Reynolds number.
But in a new study Tritton (1959) called into question that there were only two ranges of shedding, the stable and the turbulent, and directly contradicted Roshko’s results regarding the evolution of the shedding frequency with the Reynolds number. Tritton argued on the basis of new measurements for the existence of a discontinuity in the curve that displays the frequency plotted against the velocity. This discontinuity appears within the stable range, thus contradicting the linear relationship of Roshko’s formula.
In addition, Roshko’s simple division into two ranges of shedding, one stable the other turbulent, suggested that the dynamics of the wake in the stable range would be two-dimensional, contained in the plane perpendicular to the cylinder. Tritton’s visualization of the wake appeared to show, to the contrary, that the dynamics of the wake are not what Roshko’s results suggested. Beyond the discontinuity—that is, for values of Re greater than the one for which the discontinuity occurs—the shedding of the vortices along the cylinder is not simultaneous. To put it differently, the imaginary lines joining side-by-side vortices along the cylinder are not parallel to the axis of the cylinder—they are oblique.
That the successive lines of the vortices are or are not parallel to the axis of the cylinder translates in terms of the dimension of the dynamics of the wake. Parallel lines of vortices correspond to a two-dimensional dynamics of the wake. In contrast, nonparallel lines of vortices testify to the existence of a dynamics in the direction of the cylinder, which added to the two-dimensional dynamics would make the total dynamics of the wake three-dimensional. But three-dimensional effects on the dynamics were thought to be associated with the development of turbulence, which according to Roshko took place beyond the stable range.
This conflict between Roshko’s and Tritton’s experimental results started a controversy that lasted thirty years. Is or is not the discontinuity, and the oblique shedding, an intrinsic, fluid-mechanic phenomenon, irrespective of the experimental setup?
Model Implications versus Experimental Measurements
It was not until 1984 that a model of the wake was proposed to account for its temporal dynamics—that is, for the temporal evolution of the amplitude of the vortices and of the frequency at which they are emitted (Mathis, Provansal, and Boyer 1984). The model in question was obtained from the general model proposed by Landau (1944) to describe the development of a periodic instability, which he viewed as the first step toward turbulence. As illustrated in Figure I.1, the Landau model of the wake describes the amplitude of the wake in the two-dimensional plane perpendicular to the axis of the cylinder, and it predicts that the maximum amplitude is proportional to the difference between the Reynolds number (Re) and its critical value (Rec):
U 2ymax ∝ (Re − Rec)
The measurements of the amplitude that were made showed that, in this respect, the model works beautifully—even better than expected. So for the evolution of the amplitude, at least, one and the same model can account for the development of the instability on the whole range of the Reynolds number. This result contradicts Tritton’s claim that two different instabilities are at play on two ranges of Reynolds number.
But the same model also predicts that the evolution of the frequency with the Reynolds number is linear, with no discontinuity! Yet the measurement results continue to show the existence of a discontinuity. And additional measurements made along the cylinder indicate the existence of a three-dimensional dynamics, an oblique shedding.
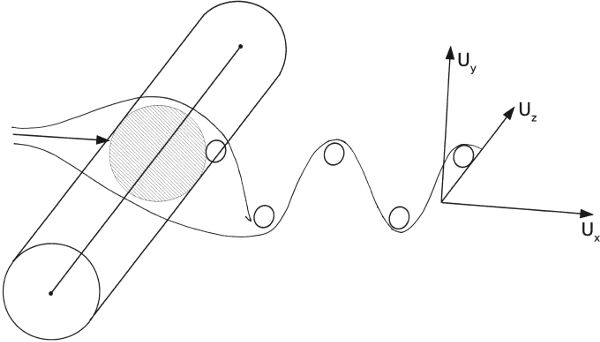
Figure I.1. Two-dimensional geometry: cross-section of the cylinder. (Courtesy P. Le Gal. Adapted by Nousoul Digital Publishers.)
Analysis: Back to Questions of Interpretation
Does the discrepancy between the model’s prediction of the evolution of the frequency and the outcomes of measurement show or even indicate that the Landau model is not an adequate model for the wake? That depends. It depends on whether that discontinuity has to be accounted for by a model of the wake. If the discontinuity is an artifact, the model of the wake not only does not have to account for it, but should not account for it. On the other hand, if it is an intrinsic feature of the wake, a model that does not account for it cannot, in that context, count as a model of the wake.
The problem is not one of data analysis or of construction of what is usually referred to, after Suppes (1962), as “models of the data.” The main problem can be posed apart from that. Even if procedures of analysis are assumed to be in place and a data model is produced—a data model of the evolution of the shedding frequency with Re—we are still left with an open question: Is this data model one that the model of the wake should match?
This has the form of a normative question. How is it settled in practice? Since it was in fact settled in practice, the subsequent history provides us with an instructive lesson in how fact and normativity interact in scientific inquiry.
Intrinsic Characteristics and Relevant Parameters
Williamson (1989) described the controversy as a search to determine “whether the discontinuity is an intrinsic, fluid-mechanic phenomenon, irrespective of the experimental setup.” The idea of being irrespective of the experimental setup seems to offer an empirical criterion to distinguish genuine data—data that are informative about the target phenomenon—from uninformative data, including artifacts. If the discontinuity is intrinsic, it should not depend on the experimental setup; if it is shown to depend on the experimental setup, then it is not intrinsic. This motivated experimental studies of the effect of an increase of the non-uniformities in the flow or in the diameter, as well as of the effect of making a cylinder vibrate. In each case, the idea was to show that the discontinuity is generated by some specific features of the experimental setup and consequently is not a feature of the wake itself.
It is not sufficient, however, to show that the discontinuity is only the effect of non-uniformities or vibrations. It would also have to be shown that without non-uniformities or vibrations there is no discontinuity. This is precisely the challenge that some numerical studies were going to try to address.
Simulation of the Wake
It is not easy to show that when there is no non-uniformity or no vibration there is no discontinuity. Both flowing fluid and the diameter of a cylinder keep a certain level of non-uniformity, however carefully they are prepared. Fortunately, by the end of the 1980s the situation of the wake lent itself to the modern alternative: numerical simulation.
A simulation of the Navier–Stokes equations, which are fundamental equations in fluid mechanics, was performed to find out how the flow behind a cylinder develops when there are no non-uniformities of any sort and no vibration (Karniadakis and Triantafyllou 1989). The results of the simulation were presented as pointing to a definite answer to the question of the nature of the discontinuity. And once again, as with the Landau model, the answer was that the evolution of the frequency with Re is linear, with no discontinuity.
These results certainly show that the occurrence of the discontinuity in the experiments results from the influence of some “additional” factors that are not taken into account as parameters of the system in the Navier–Stokes equations, as applied to this setup in the simulation. But the parameters of Navier–Stokes are those whose effect is constitutive of fluid-mechanical phenomena. So if one trusts the method used for the simulation (a spectral-element method, used successfully in previous studies) and does not envisage calling into question the validity of the fundamental equations, the most obvious conclusion would be that the effect of these additional factors constitutes an artifact and should therefore be shielded.
This conclusion about the discontinuity only holds, however, under certain assumptions. For the results to be relevant to the understanding of this phenomenon, the simulation must be an imitation, an accurate mimetic representation of the phenomenon we are interested in. Whether it is indeed, this is where the problem of identification of the relevant parameters sneaks in.
To speak of simulating the fundamental equations is not exactly right in at least two respects. First of all, the computer can only run a discrete model. Thus, the simulation requires the construction of a system of discrete equations and a method of discretization for time and space to obtain the simulation model. As Lenhard (2007) shows, the construction of the simulation model may become a modeling process in its own right, when the norm that guides and regulates the construction is precisely in agreement with the observations of the phenomenon in question. The main normative requirement being the successful imitation, the simulation model may be as far from the theoretical model as from a phenomenological model.
Something else may be overlooked when one speaks of simulating the fundamental equations, something that is independent of the way in which the simulation model is obtained. The fundamental equations are abstract, and going from the fundamental equations to the simulation of a target phenomenon must involve specifications that determine what particular situation is the target of the simulation.
On closer inspection, what raises doubt as to the significance of the result of the simulation is the geometry of the simulated situation. As may already have been apparent from Figure 1.1, this is a two-dimensional geometry representing a plane containing a cross section of the cylinder.
The simulation is meant to tell what the observation should be, what the phenomenon is really like, and whether the discontinuity is part of it or not. But how could this simulation of the development of a flow in a two-dimensional plane tell what it is like when a flow goes around a cylinder and develops in a space that contains not only the plane perpendicular to the axis of the cylinder but also the plane that contains that axis?
There is an assumption that answers this question. It is the assumption that with respect to the phenomenon under study (the frequency of shedding of the vortices forming the wake) all points on the cylinder are in relevant respects equivalent to one another, that “the same thing happens everywhere.” With that assumption in place, there is no need to simulate the wake in each point of the cylinder; any cross section will suffice.
What the two-dimensional simulation shows then is how the wake develops, according to the Navier–Stokes equations, in conditions where all the points on the cylinder are relevantly interchangeable. But why should we think that all the points are interchangeable? The presence of the ends obviously creates an asymmetry contradicting the assumptions of the simulation.
To this question too there is an answer. Suppose that a cylinder that is long enough can be regarded as infinite, as a cylinder that has no end. If there is no end, then we are in the situation where all points are interchangeable. All that is needed to satisfy this assumption of an infinite cylinder is that, for a long enough cylinder, what happens in the middle part of the cylinder be independent from what happens at or near the ends. And it could then be admitted that the two-dimensional simulation will, at least, show what should happen in a long enough cylinder, far enough from the ends.
Taking the simulation as relevant is, consequently, taking the ends of the cylinder as being irrelevant to the understanding of the fluid-mechanical features, amplitude or frequency, of the wake. Another way to put this: so regarded, the ends of the cylinder are treated in the same way as non-uniformities of the flow or vibrations of the cylinder. If they have an effect on the outcomes of measurement, this effect will be classified as an artifact and should be shielded.
Thus, the implicitly made assumption is that the ends are taken not to be a relevant parameter of the system, and that the effects on the dynamics of the wake that are due to a finite cylinder having ends are not intrinsic characteristics of the dynamics.
Experimental Contribution to Conceptual Understanding
This assumption about the ends of the cylinder would be temporarily supported by measurements that had shown that for a long enough cylinder the frequency of shedding in the middle of the cylinder is different from that found near the ends. But that should not mislead us into thinking that the assumption was an empirical assumption. The assumption is normative, in that it specifies the “normal” conditions of development of the wake, the conditions where it has its “pure” form. With this in place, the conditions under which the ends would have an effect on the measurement results would simply not count as the proper conditions of measurement.
There was for the experimenter an additional assumption in place: that the difference between a finite cylinder and one with no ends depends just on the length of the cylinder. Concretely, this implies the assumption that the way to shield off the effect of the ends is to have a sufficient length.
These two assumptions were called into question by Williamson (1989) in a thoroughgoing experimental study of the evolution of the shedding frequency, which was a turning point for our understanding of the discontinuity and the development of three-dimensional effects.
Measurements of the shedding frequency with a probe moving along the span of the cylinder showed the existence of different regions characterized by different shedding frequencies. In particular, a region of lower frequency was found near the ends. More precisely, for a cylinder with an aspect ratio (the ratio L/D of the length to the diameter) beyond a specific value, the frequency near the ends differed from the frequency in the central region. “This suggests,” Williamson wrote, “that the vortex shedding in the central regions of the span is unaffected by the direct influence from the end conditions” (Williamson 1989, 590; italics added). Note, however, that Williamson recognized only the absence of a direct influence.
Why did Williamson underline the absence only of a direct influence of the ends on the wake in the central region? In the case where there was a difference in frequency between the ends and the central part of the cylinder, visualizations of the temporal development of the wake along the cylinder were made. They showed that, initially, the lines of vortices traveling downstream were parallel to the cylinder and that progressively the parallel pattern was transformed into a stable oblique pattern, which propagated from the ends of the cylinder toward the central region. These observations suggested that there is an effect propagated toward the center. If so, this could be attributed to an influence of the ends, which is indirect in that it is not on the value of the frequency itself. But whether this influence should be part of our understanding of the wake would still be a question.
So far, all the observations and measurements had been made with endplates perpendicular to the axis of the cylinder. But with this new focus on the possibility of effects due to the ends, further measurements were made for different values of the angle between the axis of the cylinder and the plates. And, lo and behold, for a certain angle the shedding becomes parallel—that is, two-dimensional—and the discontinuity disappears, even though the length did not change.
Changing the angle of the plates has the effect of changing the pressure conditions responsible for the existence of a region of lower frequency toward the ends. When there is such a region of lower frequency, a phase difference propagates from the ends toward the central region, and this propagation creates the pattern of oblique shedding. For a certain interval of angles of the endplates, when the pressure and the vortex frequency match those values over the rest of the span, there is no region of lower frequency and no propagation of phase difference, and the shedding is parallel. The infamous discontinuity only appears in the oblique mode of shedding and is found to correspond to the transition of one oblique pattern to another with a slightly different geometry.
Analysis: An Interactive, Creative, Open-Ended Process
Williamson takes his results to “show that [the oblique and parallel patterns] are both intrinsic and are simply solutions to different problems, because the boundary conditions are different” (1989, 579). The two forms of shedding correspond to different values of the angle between the endplates and the axis of the cylinder. If no special status is bestowed on certain values of this angle in contrast to the others, there is no reason to take only one of the shedding patterns as being normal or intrinsic. In this new perspective, the parallel and the oblique pattern are not two distinct phenomena, with only one being the normal form of the wake. They are two possible configurations of the flow corresponding to different values of a parameter of the experimental system, two possible solutions for the same system in different conditions.
But this new way of seeing implies that the two assumptions, on which the relevance of the simulation depended, must be rejected. First, a new parameter should be added to the set of relevant parameters of the system, namely, one that characterizes the end conditions of the cylinder. This is to insist that the phenomenon under study is a process involving a finite cylinder because exactly finite cylinders are ones with ends; the effect that the end conditions have on the development of the wake is now part of the structural characteristics of the wake. Second, this parameter is independent of the length of the cylinder. The difference between the ends and the central part needs to be reconceived in terms of pressure difference and the value of the angle of the end plates that determines the value of this pressure difference.
By integrating this parameter among the set of relevant parameters the gain is one of conceptual unification: what were seen as two distinct phenomena have been unified under the same description. To integrate the ends among the relevant factors through the definition of a new relevant parameter and not to bestow a special status on a particular range of values of the angle are normative transformations of the investigation.
To sum up, the elaboration of an experimental system is an interactive, creative, open-ended process and contributes constructively to the processes of modeling and simulating. The constructive contribution is mediated by the identification of the relevant parameters. The relevant parameters are characteristics of the experimental system such that not only does their variation have an effect on the phenomenon but this effect is constitutive of the phenomenon—intrinsic to the phenomenon. As we have seen, the classification of characteristics into intrinsic versus interference or artifact is not there beforehand; it is during the inquiry, with its successive steps of experiment and model construction, that the phenomenon is identified. To paraphrase a line from a quite different philosophical scene, the phenomenon under study is what it will have been: what was studied is what it is seen to have been in retrospect.
The identification of the relevant parameters is required for determining the conditions in which measurements provide the empirical touchstone of a putative model of the phenomenon. Before that, a putative model is untestable. The specification of the relevant parameters involves a systematic empirical investigation of the effects of different factors, but the line that is drawn between which effects are relevant and which are not is normative. The effects of the relevant parameters are those a model of the phenomenon should account for. The criterion of relevance and the consequent criteria of adequacy for modeling determine the normative “should.”
We had an interactive process in that both the predictions of a still untestable model and the results of a prejudiced simulation contributed to shaping the experimental search for the relevant parameters. The new relevant parameter that was introduced in the conception of the phenomenon amounted to a conceptual innovation. The process of mutually entangled steps of experimentation and modeling is a creative process.
And it is open ended. A new model was formulated in response to the reconception of the phenomenon. Immediately, the exactitude of some of Williamson’s measurements was called into question on the basis of an analysis of the solutions of that new model. New measurements were to follow as well as new simulations and a modified version of the model, and so it goes on.[7]
Models of Experiments and Models of Data
An experiment is a physical, tangible realization of a data-generating procedure, designed to furnish information about the phenomena to which a theoretical model or hypothesis pertains. But while it is correct that the experiment and the procedure performed are physical and tangible, it would be thoroughly misleading to regard them merely as thus. The experimenter is working with a model of the instrumental setup, constructed following the general theoretical models afforded in the theoretical background.
Model of the Experiment
In Pierre Duhem’s The Aim and Structure of Physical Theory (1914/1962) we find our first inspiring effort to describe the interactive practice that constitutes the experimental side of modeling. Duhem describes graphically the synoptic vision required of the experimenting scientist:
When a physicist does an experiment, two very distinct representations of the instrument on which he is working fill his mind: one is the image of the concrete instrument that he manipulates in reality; the other is a schematic model of the same instrument, constructed with the aid of symbols supplied by theories; and it is on this ideal and symbolic instrument that he does his reasoning, and it is to it that he applies the laws and formulas of physics. (153–54)
This is then illustrated with Regnault’s experiment on the compressibility of gases:
For example, the word manometer designated two essentially distinct but inseparable things for Regnault: on the one hand, a series of glass tubes, solidly connected to one another, supported on the walls of the tower of the Lycée Henri IV, and filled with a very heavy metallic liquid called mercury by the chemists; on the other hand, a column of that creature of reason called a perfect fluid in mechanics, and having at each point a certain density and temperature defined by a certain equation of compressibility and expansion. It was on the first of these two manometers that Regnault’s laboratory assistant directed the eyepiece of his cathetometer, but it was to the second that the great physicist applied the laws of hydrostatics. (156–57)
We would say it somewhat differently today, if only to place less emphasis on the instrument than on the setup as a whole. But Duhem’s insight is clear: the scientist works both with the material experimental arrangement and, inseparably, indissolubly, with a model of it closely related to, though generally not simply derived from, a theoretical model.
Experiment as DATA-GENERATING Procedure
For the modeling of phenomena, what needs to be explored and clarified is the experimental process through which theoretical models or hypotheses about phenomena get “connected” to the world through the acquisition of data. Several steps in this process need to be distinguished and analyzed.
As Patrick Suppes made salient meanwhile, it is not just the model of the experimental setup that appears in the experiment’s progress (Suppes 1962, 2002). The experiment is a data-generating procedure, and the experimenter is constructing a data model: “The concrete experience that scientists label an experiment cannot itself be connected to a theory in any complete sense. That experience must be put through a conceptual grinder . . . [Once the experience is passed through the grinder,] what emerges are the experimental data in canonical form” (Suppes 2002, 7). Thus, we see alongside the model of the experimental setup and the model of the phenomenon a third level of modeling: the modeling of the data. But as Suppes emphasized, even that is an abstraction because many levels within levels can be distinguished.
We find ourselves today a good century beyond Duhem’s introduction to the modeling of experiments and a good half-century beyond Suppes’s spotlight on the data model. In those seminal texts we see a conceptual development that was far from over. Unexpected complexities came to light in both aspects of the interactive process of experimentation and modeling.
Construction of the Data Model, Then and Now
To show how data models are constructed we will select two examples from experimental work in physics, approximately one hundred and twenty years apart, so as to highlight the commonality of features in modern experimental work.[8] The first example will be Albert A. Michelson’s 1879 experiment at the Naval Academy to determine the velocity of light. As second illustration we have chosen a contemporary article in fluid mechanics, Cross and Le Gal’s 2002 experiment to study the transition to turbulence in a fluid confined between a stationary and a rotating disk. In both these experiments, the reported results consist of the data generated, presented in (quite differently displayed) summary “smoothed” form but with ample details concerning the raw data from which the data model was produced.
Michelson on Determination of the Velocity of Light
The terrestrial determination of the velocity of light was one of the great experimental problems of the nineteenth century. Two measurement results were obtained by Fizeau’s toothed wheel method, by Fizeau in 1849 and by Cornu in 1872. Between these, Foucault had obtained a result in 1862 that was of special interest to Michelson.
A schematic textbook description of Foucault’s apparatus sounds simple: a beam of light is reflected off a rotating mirror R to a stationary mirror M, whence it returns to R, and there it is reflected again in a slightly different direction because R has rotated a bit meanwhile. The deflection (the angle between the original and new direction of the beam) is a function of three factors: the distance between the mirrors, the rotational velocity of R, and the speed of light. The first two being directly measurable, the latter can be calculated.
But this omits an important detail. There is a lens placed between R and M to produce an image of the light source on M. That image moves across M as R rotates, and if the distance is to be increased (so as to increase the deflection), mirror M must be made larger. Foucault managed to increase the distance to about sixty-five feet, but that left the deflection still so small that the imprecision in its measurement was significant.
Michelson realized that by placing the light source at the principal focus of the lens he would produce the light beam as a parallel bundle of rays, and that could be reflected back as a parallel beam by a plane mirror placed at any desired distance to the rotating mirror. Even his first setup allowed for a distance of 500 feet, with a deflection about twenty times larger than in Foucault’s. The experiment in 1879 improved significantly on that, and the value he obtained was within 0.0005 km/second of the one we have today. This value is what is reported in Michelson (1880).
So what were the data generated on which this calculation was based? They are presented in tables, with both raw data and their means presented explicitly. Michelson is careful to present their credentials as unbiased observation results, when he displays as a specimen the results noted on June 17, 1879, at sunset: “the readings were all taken by another and noted down without divulging them till the whole five sets were completed.” We note that, at the same time, this remark reveals the human limits of data collection at that time, which will be far surpassed in the contemporary example we present later. The columns in Table I.1 are sets of readings of the micrometer for the deflected image. Following this specimen comes the summary of all results from June 5 through July 2, 1879; Table I.2 is a truncated version of just the first two days.
Concentrating on this part of the report omits many of the details and the ancillary reported observations, including those that serve to certify the calibration and reliability of the instruments used. For the steel tape used to measure distances, the micrometer, and the rate of the tuning fork for time measurement, the report includes a separate data-generating procedure and its results. The credentialing of the experimental setup concludes with a detailed consideration of possible sources of error, such as the possibility that the rotation of the mirror could throw the deflected light in the direction of rotation, or that the rotation of the mirror itself could cause a distortion by twisting or centrifugal force, or that there could be systematic bias in a single observer’s readings. Although just a few paragraphs are devoted to the theory (in effect, the previous schematic description), what is described in detail is the procedure by which the data are generated and the care and precautions to ensure reliability, issued in a summary presentation of those data and the calculated value of the speed of light.
Cross and Le Gal on Torsional Couette Flow
As so much else in fluid mechanics, the flow of a fluid between two plates, with one rotating relative to the other (Couette flow), can be modeled starting with the Navier–Stokes equations. But the study of idealized models—for example, with two infinite parallel plates, even with a pressure gradient imposed—leaves the experimenter with only clues as to what to expect in real situations of this sort.
In the study by Cross and Le Gal (2002), the subject of study was turbulence in the flow for different values of the rotation rate Ω. The gap h between the two disks could be varied continuously between 0 and 21 mm, and the rotational velocity between 0 and 200 revolutions per minute (rpm). The specific results included in the report, as presenting a typical case, were for a fixed gap of approximately 2.2 mm, with the rotation rate Ω increased by 2 rpm in steps from 42 rpm to 74 rpm.
The report of the experimental results shows the same attention to the details of the apparatus and setup that we saw in Michelson’s report, but there is a world of difference in the techniques whereby the data model is produced—as we are more than a century beyond hand-drawn tables of numbers. Figure I.2 shows the experimental device, which consists of a water-filled cylindrical housing in which the rotating disk is immersed and whose top is the stationary disk. The raw data are obtained by use of a video camera. The water is seeded with reflective anisotropic flakes to perform visualizations. The orientation of these particles depends upon the shear stress of the flow, so the structures that develop in the fluid layer can be observed. For each Ω value, the velocity of the rotating camera is chosen so that the turbulent spirals are seen as stationary to facilitate the image acquisition.
These images become the raw material for the production of the data model. The turbulent regions appear dark because of the completely disordered motion of the reflective flakes in these areas. The obtained spatiotemporal diagrams are thus composed of turbulent/dark domains inside laminar/clear ones. To extract physical characteristics, the diagrams are binarized: the disordered states appear in black, the ordered in white. The filtered images are produced from the raw images by sharpening the images, followed by a succession of “erosions” and “dilatations.”[9]
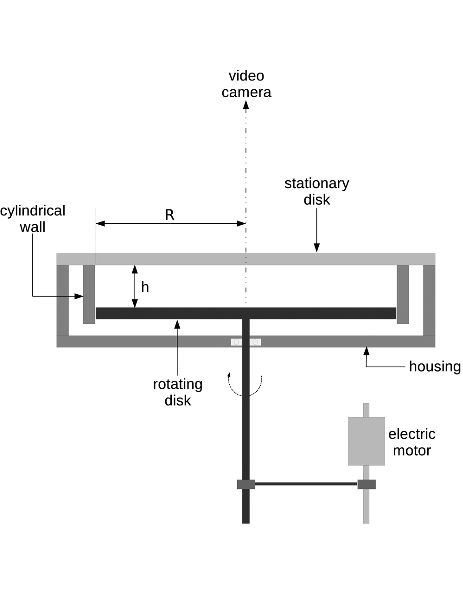
Figure I.2. Experimental setup for Couette flow. (Courtesy P. Le Gal. Adapted by Nousoul Digital Publishers.)
This procedure so far already involves a good deal of processing of the data, but it is still an intermediate step on the way to the data model that depicts the significant results. Upon increasing the rotating disk velocity Ω, a first instability results that leads to a periodic spiral wave pattern. When Ω is increased still further, this wave pattern presents some amplitude modulations and phase defects. At a second threshold, these defects trigger the turbulent spirals. As the rotation rate is increased, the lifetime of these turbulent structures increases until a threshold is reached where they then form permanent turbulent spirals arranged nearly periodically all around a circumference. However, because the number of these turbulent spirals decreases with the rotational frequency, the transition to a fully turbulent regime is not achieved. The data model thus described, constructed from a series of experiments of the type described here, is graphically and rather dramatically presented in Figure I.3.
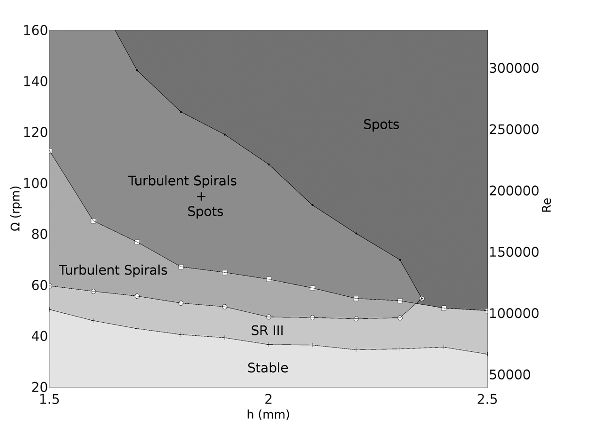
Figure I.3. Transition diagram plotting the rotation rate threshold in rpm (left axis) against the gap width to show the turbulent spirals’ appearance threshold (curves marked with o) and disappearance threshold. (Courtesy P. Le Gal. Adapted by Nousoul Digital Publishers.)
Analysis: From Singular Observation Statement to Gigabytes of Data
The difference in the procedures followed, at a concrete level, to manage large amounts of data collected not by individual observation but application of technology is clear. In this respect Michelson’s procedure is already very sophisticated, but Cross and Le Gal’s is quantitatively far beyond Michelson’s with respect to the generation, collection, recording, and statistical analysis of the data. To appreciate what is important about these two examples of experimentation, we need to appreciate their function, which is essentially the same but must be discerned within these very different technological realizations.
The data model constructed on the basis of outcomes of measurement can be viewed as the pivotal element in the experimental process. What makes the data model a pivotal element is its dual epistemic function:
- • On the one hand, the data model is supposed to be an empirical representation of the phenomenon under investigation.
- • On the other hand, the data model serves as a benchmark for the construction and evaluation of the theoretical model of (or theoretical hypothesis about) the phenomenon.
Given the pivotal function of the data model, to investigate the experimental process that connects theoretical models to phenomena is to clarify the different steps that lead to the construction and interpretation of data models:
- • The formulation of a model of the experiment, specifying what needs to be measured (motivated and guided by a preconception of the phenomenon under investigation and, in some cases, a putative theoretical model of this phenomenon).
- • The realization and interpretation of measurement operations according to the specifications of the model of the experiment.
- • The construction of data models on the basis of the outcomes of measurement.
- • The interpretation of the data models, as repository of information about phenomena.
- • The use of data models to construct or produce evidence for/against the theoretical model offered as putative theoretical representation of the phenomenon.
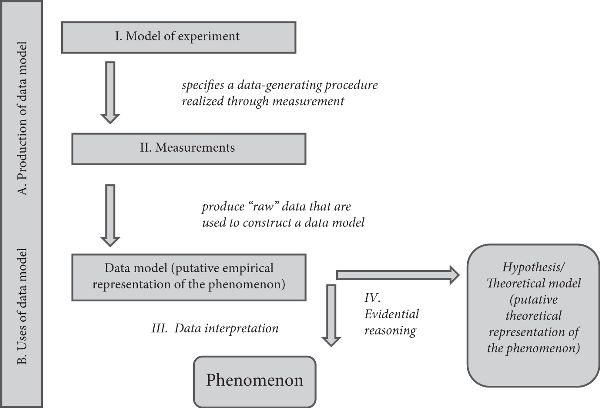
Figure I.4. The experimental process diagrammatically displayed.
The arrows in Figure I.4 do not represent temporal order. To put it bluntly, even paradoxically, experimentally based modeling starts neither with a model to be tested nor with a data-generating procedure. It starts with a problem for which relevant data need to be produced and evidentially supported models need to be constructed. The different stages in this process, from the abstract terms of the problem to the specification and realization of experimental procedures, from issues about evidential relevance to an explication of the similarity relation between models and data, are the subject of the contributions in this collection.
The Experimental Side of Modeling Philosophically Approached
The philosophical essays on modeling and experimentation in this volume are representative of the current literature in the philosophy of science in many ways: in their diversity of approach, in the tensions between them, and in the differences in focus that divide them. One crucial and central concern is found in all of them—the most striking, groundbreaking result perceivable in these contributions is their radically new conception of the role of data in the modeling process. Specifically, they have a new awareness of what is problematic about data. Instead of being a passive element of modeling or experimenting, already standing ready to act the role of tribunal or simply flowing from an experimental procedure, data have become the central point of the experimentally based modeling process. Data are both what need to be produced and what need to be accounted for to create the prospect for articulation of both the theoretical model and the model of the experiment. Data are the manifestation of the phenomenon under study, they are what needs to be interpreted, and their very relevance or significance itself becomes the issue.
Notes
1. Logical terminology is typically foreign to the background mathematical practice: a set of models that is precisely thus, the set of models that satisfy a given set of sentences, is in logical terminology an elementary class. But let us not let differences of jargon obscure that the logicians’ “model” is just a straightforwardly generalized concept coming from ordinary mathematical practice familiar to the scientist.
2. Reflecting on her journey from 1983 to 1995, in a later article Cartwright wrote, “I have been impressed at the ways we can put together what we know from quantum mechanics with much else we know to draw conclusions that are no part of the theory in the deductive sense” (1999, 243). The point is, of course, not that one cannot deduce all consequences of a conjunction from one conjunct—obviously—but rather to draw attention to the cooperation with other input so saliently, importantly needed in actual practice.
3. Superconductivity presented an instructive example. A much earlier example in the literature that should already have made the point glaringly clear was Jon Dorling’s 1971 analysis of how Einstein arrived at the photon model of light.
4. See also appendix 1 of van Fraassen (2008).
5. For a more comprehensive version of this section, see Peschard (2010).
6. Indeed, to Margaret Morrison (2009) it did not seem inapt to say that models, including those models that are simulation programs on computers, can function as measuring instruments. But this was certainly more controversial, especially for computer simulations. There is definitely an understanding of models as having a role in experimenting and measuring that does not make them measuring instruments (cf. Peschard 2013; Parke 2014).
7. For the larger story, see further Peschard (2011a).
8. The term “data model” as we currently use it in the philosophy of science derives from the seminal writings by Patrick Suppes. This usage is to be distinguished from its use in other fields such as software engineering in database construction for business and industry.
9. The erosion is the elimination of a black pixel if a chosen number s or more of white pixels is found among its eight neighbors. A dilatation is the inverse transformation: a white pixel is transformed to black if it is surrounded by a number s′ or more of black pixels. Here, s, s′ were set at 2. The first step is an erosion in order to eliminate the undesirable black dots from noise. Then seven successive dilatations and a final erosion achieve a visual aspect of the binarized diagrams relevantly equivalent to the original ones.
References
Barberousse, Anouk, Sara Franceschelli, and Cyrille Imbert. 2009. “Computer Simulations as Experiments.” Synthese 169: 557–74.
Barwich, Ann-Sophie, and Hasok Chang. 2015. “Sensory Measurements: Coordination and Standardization.” Biological Theory 10: 200–211.
Bogen, James, and James Woodward. 1988. “Saving the Phenomena.” Philosophical Review 98: 303–52.
Carnap, Rudolf. 1928. Der logische Aufbau der Welt. Berlin-Schlachtensee: Weltkreis Verlag.
Cartwright, Nancy. 1979. “Causal Laws and Effective Strategies.” Noûs 13 (4): 419–37.
Cartwright, Nancy D. 1983. How the Laws of Physics Lie. Oxford: Clarendon Press.
Cartwright, Nancy D. 1999. “Models and the Limits of Theory: Quantum Hamiltonians and the BCS Models of Superconductivity.” In Models as Mediators: Perspectives on Natural and Social Science, edited by Mary S. Morgan and Margaret Morrison, 241–81. Cambridge: Cambridge University Press.
Cartwright, Nancy D. 2014. “Measurement.” In Philosophy of Social Science. A New Introduction, edited by N. Cartwright and E. Montuschi, 265–87. New York: Oxford University Press.
Cartwright, Nancy D., T. Shomar, and M. Suárez. 1995. “The Tool Box of Science.” In Theories and Models in Scientific Processes, edited by W. Herfel, W. Krajewski, I. Niiniluoto, and R. Wojcicki, 137–49. Amsterdam: Rodopi.
Cross, Anne, and Patrice Le Gal. 2002. “Spatiotemporal Intermittency in the Torsional Couette Flow between a Rotating and a Stationary Disk.” Physics of Fluids 14: 3755–65.
Dorling, Jon. 1971. “Einstein’s Introduction of Photons: Argument by Analogy or Deduction from the Phenomena?” British Journal for the Philosophy of Science 22: 1–8.
Duhem, Pierre. (1914) 1962. The Aim and Structure of Physical Theory. Translated by Philip P. Wiener. New York: Atheneum. First published as La Théorie physique, son objet, sa structure (Paris: Marcel Rivière & Cie, 1914).
Friedman, Michael. 1999. Reconsidering Logical Positivism. Cambridge: Cambridge University Press.
Giere, Ronald N. 2009. “Is Computer Simulation Changing the Face of Experimentation?” Philosophical Studies 143: 59–62.
Halvorson, Hans. 2012. “What Scientific Theories Could Not Be.” Philosophy of Science 79: 183–206.
Halvorson, Hans. 2013. “The Semantic View, if Plausible, Is Syntactic.” Philosophy of Science 80: 475–78.
Humphreys, Paul. 2004. Extending Ourselves: Computational Science, Empiricism, and Scientific Method. Oxford: Oxford University Press.
Karniadakis, G. E., and G. S. Triantafyllou. 1989. “Frequency Selection and Asymptotic States in Laminar Wakes.” Journal of Fluid Mechanics 199: 441–69.
Knuuttila, Tarja, and Andrea Loettgers. 2014. “Varieties of Noise: Analogical Reasoning in Synthetic Biology.” Studies in History and Philosophy of Science Part A 48: 76–88.
Kuhn, Thomas S. 1962. The Structure of Scientific Revolutions. International Encyclopedia of Unified Science, vol. 2, no. 2. Chicago: University of Chicago Press.
Kuhn, Thomas S. 1992. “Presidential Address: Introduction.” In PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association 1992 (2): 3–5.
Landau, L. 1944. “On the Problem of Turbulence.” Comptes Rendus Académie des Sciences U.S.S.R. 44: 311–14.
Lenhard, Johannes. 2007. “Computer Simulation: The Cooperation between Experimenting and Modeling.” Philosophy of Science 74: 176–94.
Lewis, David K. 1970. “How to Define Theoretical Terms.” Journal of Philosophy 67: 427–46.
Lewis, David K. 1983. “New Work for a Theory of Universals.” Australasian Journal of Philosophy 61: 343-377.
Lloyd, Elisabeth A. 1994. The Structure and Confirmation of Evolutionary Theory. 2nd ed. Princeton, N.J.: Princeton University Press.
Mathis, C., M. Provansal, and L. Boyer. 1984. “The Benard-Von Karman Instability: An Experimental Study near the Threshold.” Journal de Physique Lettres 45: L483–91.
Michelson, Albert A. 1880. “Experimental Determination of the Velocity of Light: Made at the U.S. Naval Academy, Annapolis.” In Astronomical Papers of the U.S. Nautical Almanac 1, Part 3, 115–45. Washington, D.C.: Nautical Almanac Office, Bureau of Navigation, Navy Department. http://www.gutenberg.org/files/11753/11753-h/11753-h.htm.
Miyake, Teru. 2013. “Underdetermination, Black Boxes, and Measurement.” Philosophy of Science 80: 697–708.
Miyake, Teru. 2015. “Reference Models: Using Models to Turn Data into Evidence.” Philosophy of Science 82: 822–32.
Montague, Richard. 1957. “Deterministic Theories.” In Decisions, Values and Groups, edited by D. Wilner and N. F. Washburne, 325–70. New York: Pergamon. Reprinted in Formal Philosophy: Selected Papers of Richard Montague, edited by Richmond Thomason (New Haven, Conn.: Yale University Press, 1974).
Morgan, Mary, and Margaret Morrison, eds. 1999. Models as Mediators: Perspectives on Natural and Social Science. Cambridge: Cambridge University Press.
Morrison, Margaret. 1999. “Models as Autonomous Agents.” In Models as Mediators: Perspectives on Natural and Social Science, edited by Mary S. Morgan and Margaret Morrison, 38–65. Cambridge: Cambridge University Press.
Morrison, Margaret. 2009. “Models, Measurement and Computer Simulations: The Changing Face of Experimentation.” Philosophical Studies 143: 33–57.
Morrison, Margaret. 2015. Reconstructing Reality: Models, Mathematics, and Simulations. Oxford: Oxford University Press.
Morrison, Margaret, and Mary S. Morgan. 1999. “Models as Mediating Instruments.” In Models as Mediators: Perspectives on Natural and Social Science, edited by Mary S. Morgan and Margaret Morrison, 10–37. Cambridge: Cambridge University Press.
Parke, E. C. 2014. “Experiments, Simulations, and Epistemic Privilege.” Philosophy of Science 81: 516–36.
Parker, Wendy S. 2009. “Does Matter Really Matter? Computer Simulations, Experiments and Materiality.” Synthese 169: 483–96.
Peschard, Isabelle. 2010. “Target Systems, Phenomena and the Problem of Relevance.” Modern Schoolman 87: 267–84.
Peschard, Isabelle. 2011a. “Making Sense of Modeling: Beyond Representation.” European Journal for Philosophy of Science 1: 335–52.
Peschard, Isabelle. 2011b. “Modeling and Experimenting.” In Models, Simulations, and Representations, edited by P. Humphreys and C. Imbert, 42–61. New York: Routledge.
Peschard, Isabelle. 2012. “Forging Model/World Relations: Relevance and Reliability.” Philosophy of Science 79: 749–60.
Peschard, Isabelle. 2013. “Les Simulations sont-elles de réels substituts de l’expérience?” In Modéliser & simuler: Epistémologies et pratiques de la modélisation et de la simulation, edited by Franck Varenne and Marc Siberstein, 145–70. Paris: Editions Materiologiques.
Putnam, Hilary. 1962. “What Theories Are Not.” In Logic, Methodology and Philosophy of Science: Proceedings of the 1960 International Congress, edited by E. Nagel, P. Suppes, and A. Tarski, 240–51. Stanford, Conn.: Stanford University Press. Reprinted in Mathematics, Matter and Method. Philosophical Papers, 215–27, vol. 1 (Cambridge: Cambridge University Press, 1979).
Richardson, Alan. 1997. Carnap’s Construction of the World: The Aufbau and the Emergence of Logical Empiricism. Cambridge: Cambridge University Press.
Roshko, Anatol. 1954. On the Development of Turbulent Wakes from Vortex Streets. Washington, D.C.: National Advisory Committee for Aeronautics. http://resolver.caltech.edu/CaltechAUTHORS:ROSnacarpt1191
Russell, Bertrand. 1914. Our Knowledge of the External World: A Field for Scientific Method in Philosophy. Chicago: Open Court.
Russell, Bertrand. 1917. “Mysticism and Logic.” In Mysticism and Logic and Other Essays, 1–32. London: George Allen & Unwin. https://www.gutenberg.org/files/25447/25447-h/25447-h.htm
Russell, Bertrand. 1927. The Analysis of Matter. London: Allen & Unwin.
Ryckman T. A. 2005. The Reign of Relativity: Philosophy in Physics 1915–1925. New York: Oxford University Press.
Suárez, Mauricio. 1999. “Theories, Models and Representations.” In Model-Based Reasoning in Scientific Discovery, edited by L. Magnani, N. Nersessian, and P. Thagard, 75–83. Dordrecht, the Netherlands: Kluwer Academic.
Suárez, Mauricio. 2003. “Scientific Representation: Against Similarity and Isomorphism.” International Studies in the Philosophy of Science 17: 225–44.
Suppe, Frederick Roy. 1967. On the Meaning and Use of Models in Mathematics and the Exact Sciences, PhD diss., University of Michigan.
Suppe, Frederick Roy. 1974. The Structure of Scientific Theories. Urbana: University of Illinois Press.
Suppe, Frederick Roy. 2000. “Understanding Scientific Theories: An Assessment of Developments, 1969–1998.” Philosophy of Science 67 (Proceedings): S102–15.
Suppes, Patrick. 1962. “Models of Data.” In Logic, Methodology and Philosophy of Science: Proceedings of the 1960 International Conference, edited by E. Nagel, P. Suppes, and A. Tarski, 252–61. Stanford, Calif.: Stanford University Press.
Suppes, Patrick. 1967. Set-Theoretical Structures in Science. Stanford: Institute for Mathematical Studies in the Social Sciences, Stanford University.
Suppes, Patrick. 2002. “Introduction.” In Representation and Invariance of Scientific Structures, 1–15. Stanford, Calif.: Center for the Study of Language and Information. http://web.stanford.edu/group/cslipublications/cslipublicationspdf/1575863332.rissbook.pdf
Tal, Eran. 2011. “How Accurate Is the Standard Second?” Philosophy of Science 78: 1082–96.
Tal, Eran. 2012. The Epistemology of Measurement: A Model-Based Account, PhD diss., University of Toronto. http://hdl.handle.net/1807/34936
Tal, Eran. 2013. “Old and New Problems in Philosophy of Measurement.” Philosophy Compass 8: 1159–73.
Tritton, D. J. 1959. “Experiments on the Flow Past a Circular Cylinder at Low Reynolds Numbers.” Journal of Fluid Mechanics 6: 547–67.
Van Fraassen, Bas C. 1970. “On the Extension of Beth’s Semantics of Physical Theories.” Philosophy of Science 37: 325–34.
Van Fraassen, Bas C. 1972. “A Formal Approach to the Philosophy of Science.” In Paradigms and Paradoxes: The Challenge of the Quantum Domain, edited by R. Colodny, 303–66. Pittsburgh: University of Pittsburgh Press.
Van Fraassen, Bas C. 2008. Scientific Representation: Paradoxes of Perspective. Oxford: Oxford University Press.
Van Fraassen, Bas C. 2011. “A Long Journey from Pragmatics to Pragmatics: Response to Bueno, Ladyman, and Suarez.” Metascience 20: 417–42.
Van Fraassen, Bas C. 2012. “Modeling and Measurement: The Criterion of Empirical Grounding.” Philosophy of Science 79: 773–84.
Van Fraassen, Bas C. 2014a. “One or Two Gentle Remarks about Halvorson’s Critique of the Semantic View.” Philosophy of Science 81: 276–83.
Van Fraassen, Bas C. 2014b. “The Criterion of Empirical Grounding in the Sciences.” In Bas van Fraassen’s Approach to Representation and Models in Science, edited by W. J. Gonzalez, 79–100. Dordrecht, the Netherlands: Springer Verlag.
Weisberg, Michael. 2013. Simulation and Similarity: Using Models to Understand the World. New York: Oxford University Press.
Whitehead, Alfred North, and Bertrand Russell. 1910–13. Principia Mathematica, 3 vols. Cambridge: Cambridge University Press.
Williamson, C. H. K. 1989. “Oblique and Parallel Modes of Vortex Shedding in the Wake of a Circular Cylinder at Low Reynolds Number.” Journal of Fluid Mechanics 206: 579–627.
Winsberg, Eric. 2009. “Computer Simulation and the Philosophy of Science.” Philosophy Compass 4/5: 835–45.
Winsberg, Eric. 2010. Science in the Age of Computer Simulation. Chicago: University of Chicago Press.